3. 有一张矩形纸片ABCD,AB= 10 cm,BC= 15 cm.按如图所示方式将它剪去两部分,分别是正方形纸片AEQP和正方形纸片PGHF,且BE= DF.若余下部分的面积是原矩形纸片面积的一半,则DF= ______
$10-5\sqrt{2}$
.
答案:$10-5\sqrt{2}$.
解析:
设$DF = x\ cm$,则$BE = DF = x\ cm$。
因为四边形$AEQP$是正方形,$AB = 10\ cm$,所以$AE = AB - BE = 10 - x\ cm$,即正方形$AEQP$的边长为$10 - x\ cm$,其面积为$(10 - x)^2\ cm^2$。
矩形$ABCD$中,$AD = BC = 15\ cm$,$AP = AE = 10 - x\ cm$,所以$PF = AD - AP - DF = 15 - (10 - x) - x = 5\ cm$。
因为四边形$PGHF$是正方形,所以其边长为$PF = 5\ cm$,面积为$5^2 = 25\ cm^2$。
原矩形面积为$AB × BC = 10 × 15 = 150\ cm^2$,余下部分面积是原矩形面积的一半,所以剪去的两个正方形面积之和为$150 - \frac{150}{2} = 75\ cm^2$。
可得方程:$(10 - x)^2 + 25 = 75$,即$(10 - x)^2 = 50$,解得$10 - x = \pm 5\sqrt{2}$。
因为边长不能为负,所以$10 - x = 5\sqrt{2}$($10 - x = -5\sqrt{2}$舍去),则$x = 10 - 5\sqrt{2}$。
$10 - 5\sqrt{2}$
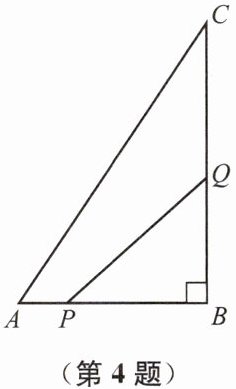
4. 如图,在△ABC中,$\angle B= 90^{\circ}$,AB= 6 cm,BC= 8 cm,点P以1 cm/s的速度从点A沿边AB向点B移动,点Q以2 cm/s的速度从点B沿边BC向点C移动(点Q到达点C运动停止).设点P、Q分别从点A、B同时出发t s($t>0$).
(1)t为何值时,PQ= 6 cm?
(2)连接PC,t为何值时,△PCQ的面积等于$3\ cm^2$?
答案:解:( 1 ) 依题意得瓷$( 6-t ) ^2+( 2t ) ^2=6^2$
解得,$t_1=0,$$t_2=2.4$
∵t>0,∴t=2.4
答:当t 为2.4时,$PQ=6\ \mathrm {cm}.$
(2)依题意得,$\frac {1}{2}( 6-t ) ( 8-2t ) =3$
解得,$t_1=3,$$t_2=7$
∵点Q到达点C运动停止
∴0<t≤4
∴t=3
答:当t为3时,△PCQ的面积等于$3\ \mathrm {cm^2}.$
5. 某海军基地位于A处,在其正南方向200 n mile处有一重要目标B,在目标B的正东方向200 n mile处有一重要目标C,小岛D恰好位于AC的中点,岛上有一补给码头;一艘军舰从A处出发,经目标B向目标C匀速巡航.一艘补给船同时从岛D出发,保持匀速直线航行(不改变方向),欲将一批物品送往军舰.已知军舰的速度是补给船的3倍,军舰在由目标B到目标C的途中与补给船相遇,求相遇处距离目标C多远.(1 n mile= 1 852 m)

答案:解:设相遇处距离目标C x海里.
依题意得,$( 200+200-x ) ^2=9[100^2+( 100-x ) ^2]$
解得,$x_1=25,$$x_2=100$
答:相遇处距离目标C 25海里或100海里.
解析:
以A为原点,正东方向为x轴正方向,正北方向为y轴正方向建立直角坐标系。则A(0,0),B(0,-200),C(200,-200),D为AC中点,坐标为(100,-100)。
设补给船速度为v,军舰速度为3v,相遇时间为t。
军舰从A到B需时间$\frac{200}{3v}$。
情况1:军舰在B到C途中相遇($t > \frac{200}{3v}$),此时军舰坐标为$(3v(t - \frac{200}{3v}), -200) = (3vt - 200, -200)$。
补给船坐标为$(100 + v t \cos\theta, -100 + v t \sin\theta)$,因相遇时坐标相同,可得:
$\begin{cases}3vt - 200 = 100 + v t \cos\theta \\-200 = -100 + v t \sin\theta\end{cases}$
由第二个方程得$v t \sin\theta = -100$,第一个方程得$v t \cos\theta = 3vt - 300$。
又$(v t \cos\theta)^2 + (v t \sin\theta)^2 = (vt)^2$,代入得:
$(3vt - 300)^2 + (-100)^2 = (vt)^2$
令$s = vt$,则$(3s - 300)^2 + 10000 = s^2$,解得$s = 100$或$s = 125$。
当$s = 100$时,$t = \frac{100}{v} < \frac{200}{3v}$(舍去,此时军舰未到B);当$s = 125$时,$t = \frac{125}{v} > \frac{200}{3v}$,军舰横坐标为$3s - 200 = 175$,距离C为$200 - 175 = 25$ n mile。
情况2:军舰在A到B途中相遇($t \leq \frac{200}{3v}$),军舰坐标为$(0, -3vt)$,补给船坐标为$(100 + v t \cos\theta, -100 + v t \sin\theta)$,相遇时:
$\begin{cases}0 = 100 + v t \cos\theta \\-3vt = -100 + v t \sin\theta\end{cases}$
解得$s = vt = 100$,$t = \frac{100}{v} < \frac{200}{3v}$,军舰横坐标为0,距离C为200 n mile(但题目明确“军舰在由目标B到目标C的途中与补给船相遇”,此情况舍去)。
综上,相遇处距离目标C 25 n mile。
25 n mile