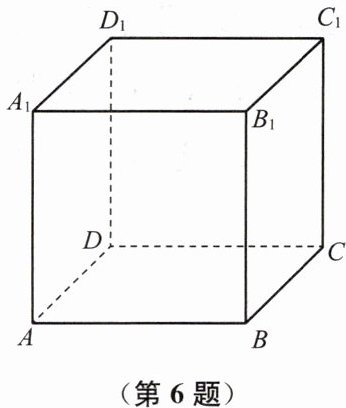
6. 如图,一个密封的正方体盒子的棱长为10 cm,在盒子内部顶点$C_1$处有一只昆虫甲,顶点A处有一只昆虫乙.假设昆虫甲从顶点$C_1$以1 cm/s的速度在盒子的内部沿$C_1C$向下爬行,同时昆虫乙从顶点A以2 cm/s的速度在内盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
答案:解:分两种情况:
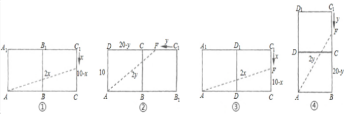
①昆虫乙经过棱$BB_1$或$DD_1$爬向昆虫
乙,如图①、③,
设昆虫乙需要$ x\ \mathrm {s}$才能捕捉到昆虫甲.
依题意得,
$( 10+10 ) ^2+( 10-x ) ^2=( 2x ) ^2$
解得,$x_1=10,$
$x_2=-\frac {50}{3}( $不合题意,舍去 )
∴x=10
②昆虫乙经过棱BCa或DC爬向昆虫
乙,如图②、④,
设昆虫乙需要$ y\ \mathrm {s}$才能捕捉到昆虫甲.
依题意得,
$10^2+( 20-y ) ^2=( 2y ) ^2$
解得,$y_1=\frac {-20+10\sqrt{19}}{3},$
$y_2=\frac {-20-10\sqrt{19}}{3}($不合题意,舍去)
∴$y=\frac {-20+10\sqrt{19}}{3}$
∵$\frac {-20+10\sqrt{19}}{3}\lt 10$
∴昆虫乙至少需要$\frac {-20+10\sqrt{19}}{3}$秒才能
捕捉到昆虫甲.
解析:
设昆虫乙捕捉到昆虫甲所需时间为$ t $秒。
昆虫甲爬行距离:$ C_1C' = 1 \cdot t = t \, cm $,则$ CC' = 10 - t \, cm $。
昆虫乙爬行距离:$ AB' = 2t \, cm $。
将正方体侧面展开,$ AB' $为直角三角形斜边,两直角边分别为$ AC = 10 + 10 = 20 \, cm $,$ CC' = 10 - t \, cm $。
由勾股定理:$ (2t)^2 = 20^2 + (10 - t)^2 $
化简得:$ 4t^2 = 400 + 100 - 20t + t^2 $
$ 3t^2 + 20t - 500 = 0 $
解得:$ t = \frac{-20 \pm \sqrt{400 + 6000}}{6} = \frac{-20 \pm \sqrt{6400}}{6} = \frac{-20 \pm 80}{6} $
舍去负根:$ t = \frac{60}{6} = 10 \, s $(此为第一种展开情况,非最短)
另一种展开方式:直角边为$ 10 \, cm $和$ 10 + (10 - t) = 20 - t \, cm $
方程:$ (2t)^2 = 10^2 + (20 - t)^2 $
$ 4t^2 = 100 + 400 - 40t + t^2 $
$ 3t^2 + 40t - 500 = 0 $
解得:$ t = \frac{-40 \pm \sqrt{1600 + 6000}}{6} = \frac{-40 \pm \sqrt{7600}}{6} = \frac{-40 \pm 20\sqrt{19}}{6} = \frac{-20 \pm 10\sqrt{19}}{3} $
取正根:$ t = \frac{10\sqrt{19} - 20}{3} \, s $
比较两种情况,$ \frac{10\sqrt{19} - 20}{3} < 10 $
故昆虫乙至少需要$ \frac{10\sqrt{19} - 20}{3} \, s $。
$\frac{10\sqrt{19}-20}{3}$
1. 解下列方程:
(1)$196x^{2}-1= 0$;
(2)$2x^{2}+3x= 3$;
(3)$x^{2}-2x= 24$;
(4)$x(2x-5)= 4x-10$;
(5)$-\frac{2}{3}y^{2}+\frac{1}{3}y+2= 0$;
(6)$(2x-3)^{2}+3(3-2x)-4= 0$.
答案:解:$196x^2=1$
$ x^2=\frac 1{196}$
$ x=±\frac 1{14}$
$ x_1=\frac 1{14},$$x_2=-\frac 1{14}$
解:$2x^2+3x-3=0$
a=2,b=3,c=-3
$ b^2-4ac=9+4×2×3=33$
$ x=\frac {-3±\sqrt {33}}4$
$ x_1=\frac {-3+\sqrt {33}}4,$$x_2=\frac {-3-\sqrt {33}}4$
解:$x^2-2x-24=0$
(x-6)(x+4)=0
x-6=0或x+4=0
$ x_1=6,$$x_2=-4$
解:(2x-5)(x-2)=0
2x-5=0或x-2=0
$ x_1=\frac 52,$$x_2=2$
解:$2y^2-y-6=0$
(2y+3)(y-2)=0
$ y_1=-\frac 32,$$y_2=2$
解:(2x-3-4)(2x-3+1)=0
(2x-7)(2x-2)=0
2x-7=0或2x-2=0
$ x_1=\frac 72,$$x_2=1$