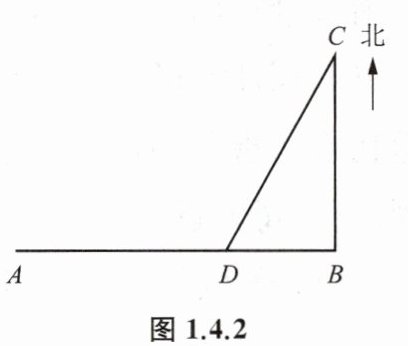
例 如图1.4.2,小岛A在码头B的正西方向,A、B两地相距40 n mile.上午9点,一渔船和一游艇同时出发,渔船以20 n mile/h的速度从B码头向正北方向出海作业,游艇以25 n mile/h的速度从小岛A返回码头B.一段时间后,渔船因故障停航在C处并发出信号,游艇在D处收到信号后直接向渔船驶去,上午11点到达C处.问游艇在上午几点收到信号?(1 n mile= 1.852 km)
答案:解:设游艇出发 x小时后收到信号.
依题意得,$( 40-25x ) ^2+( 20x ) ^2=[ 25( 11-9-x ) ] ^2$
解得,$x_1=1,$$x_2=\frac {15}{4}$
当x=1时,游艇收到信号的时间为上午10点,符合题意;
当$x=\frac {15}{4}$时,
游艇收到信号的时间已经超过上午11点,不合题意,故舍去.
答:游艇在上午10点收到信号.
解析:
设游艇在上午9点后$ t $小时收到信号。
渔船从B到C行驶时间为2小时,速度20 n mile/h,所以$ BC=20×2 = 40 $n mile。
游艇从A到D速度25 n mile/h,行驶时间$ t $小时,所以$ AD=25t $n mile,又$ AB=40 $n mile,故$ DB=AB - AD=40 - 25t $n mile。
渔船从B到C行驶$ t $小时的路程$ BC'=20t $n mile($ C' $为渔船收到信号时位置),则$ CC'=BC - BC'=40 - 20t $n mile。
游艇从D到C行驶时间为$ 2 - t $小时,路程$ DC=25(2 - t) $n mile。
在$ Rt\triangle DBC $中,$ DC^{2}=DB^{2}+BC^{2} $,即$ [25(2 - t)]^{2}=(40 - 25t)^{2}+(40 - 20t)^{2} $。
展开得:$ 625(4 - 4t + t^{2})=625t^{2}-2000t + 1600 + 400t^{2}-1600t + 1600 $
化简:$ 2500 - 2500t + 625t^{2}=1025t^{2}-3600t + 3200 $
移项合并:$ 400t^{2}-1100t + 700 = 0 $,即$ 4t^{2}-11t + 7 = 0 $
解得$ t = 1 $或$ t=\frac{7}{4} $($ t=\frac{7}{4} $时$ DB=40 - 25×\frac{7}{4}=40 - 43.75=-3.75 $舍去)
所以$ t = 1 $,即9点后1小时,上午10点收到信号。
上午10点。
1. 把一个小球以20 m/s的速度竖直向上抛出,它在空中的高度h(m)与时间t(s)满足关系式$h= 20t-5t^{2}$.当$h= 20$ m时,小球的运动时间为
2 s
.
答案:$2\ \mathrm {s}$
解析:
当$h = 20\ m$时,代入$h = 20t - 5t^{2}$,得$20 = 20t - 5t^{2}$。
整理方程:$5t^{2} - 20t + 20 = 0$,两边同时除以5,得$t^{2} - 4t + 4 = 0$。
因式分解:$(t - 2)^{2} = 0$,解得$t = 2\ s$。
2 s.
2. 如图,正方形ABCD的边长为1,点E、F分别在BC、CD上,且△AEF是等边三角形,则BE的长为
$2-\sqrt {3}$
.
答案:$2-\sqrt {3}$
解析:
设$BE=x$,则$EC=1 - x$。
因为四边形$ABCD$是正方形,所以$AB=AD=1$,$\angle B=\angle D=\angle C=90^\circ$。
由于$\triangle AEF$是等边三角形,所以$AE=AF=EF$。
在$Rt\triangle ABE$中,$AE^2=AB^2 + BE^2=1^2 + x^2=1 + x^2$。
同理,在$Rt\triangle ADF$中,设$DF=y$,则$AF^2=AD^2 + DF^2=1 + y^2$,所以$1 + x^2=1 + y^2$,即$x=y$,故$DF=x$,$FC=1 - x$。
在$Rt\triangle ECF$中,$EF^2=EC^2 + FC^2=(1 - x)^2 + (1 - x)^2=2(1 - x)^2$。
又因为$AE=EF$,所以$1 + x^2=2(1 - x)^2$,展开得$1 + x^2=2(1 - 2x + x^2)$,即$1 + x^2=2 - 4x + 2x^2$,移项化简得$x^2 - 4x + 1=0$。
解得$x=\frac{4\pm\sqrt{16 - 4}}{2}=\frac{4\pm2\sqrt{3}}{2}=2\pm\sqrt{3}$。
因为$x < 1$,所以$x=2 - \sqrt{3}$。
$2 - \sqrt{3}$