8. 小丽进行投掷标枪训练,总共投掷10次,前9次标枪的落点如图所示,此时这组成绩的平均数是20 m,方差是$s_{1}^{2}$m^2.若第10次投掷标枪的落点恰好在20 m线上,且投掷结束后这组成绩的方差是$s_{2}^{2}$m^2,试比较$s_{1}^{2}与s_{2}^{2}$的大小,并说明理由.
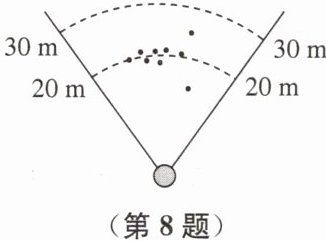
答案:$s^{2}_{1}>s^{2}_{2}$,理由略.
解析:
$s_{1}^{2}>s_{2}^{2}$,理由如下:
设前9次成绩分别为$x_{1},x_{2},\cdots,x_{9}$,第10次成绩为$x_{10}=20$。
前9次平均数$\overline{x}_{1}=20$,则$s_{1}^{2}=\frac{1}{9}\sum_{i=1}^{9}(x_{i}-20)^{2}$。
10次成绩的平均数$\overline{x}_{2}=\frac{9×20 + 20}{10}=20$,$s_{2}^{2}=\frac{1}{10}\left[\sum_{i=1}^{9}(x_{i}-20)^{2}+(20 - 20)^{2}\right]=\frac{1}{10}\sum_{i=1}^{9}(x_{i}-20)^{2}$。
因为$\frac{1}{9}\sum_{i=1}^{9}(x_{i}-20)^{2}>\frac{1}{10}\sum_{i=1}^{9}(x_{i}-20)^{2}$,所以$s_{1}^{2}>s_{2}^{2}$。
例 小明称量并记录5筐水果的质量,他以每筐50 kg为基准,超过基准部分的质量记为正数,不足基准部分的质量记为负数,把所得数据整理成如下统计表,甲组为实际称量读数,乙组为记录数据.
水果质量数据统计表
|组别|第1筐|第2筐|第3筐|第4筐|第5筐|
|甲组|48 kg|52 kg|47 kg|49 kg|54 kg|
|乙组|$-2$ kg|2 kg|$-3$ kg|$-1$ kg|4 kg|
(1) 甲、乙两组数据的平均数分别为$\overline{x}_{甲}$、$\overline{x}_{乙}$,写出$\overline{x}_{甲}与\overline{x}_{乙}$之间的等量关系;
(2) 甲、乙两组数据的方差分别为$s^{2}_{甲}$、$s^{2}_{乙}$,比较$s^{2}_{甲}与s^{2}_{乙}$的大小,并说明理由.

答案:解:$(1)\overline{x}_$甲$=\frac {48+52+47+49+54}5=50(\ \text {kg})$
$\overline{x}_$乙$=\frac {-2+2-3-1+4}5=0(\ \text {kg})$
∴$\overline{x}_$甲$=50+\overline{x}_$乙
$(2)s^2_$甲$=\frac 15×[(48-50)^2+(52-50)^2+(47-50)^2+(49-50)^2+(54-50)^2]=6.8(\ \text {kg}^2)$
$s^2_$乙$=\frac 15×[(-2)^2+2^2+(-3)^2+(-1)^2+4^2]=6.8(\ \text {kg}^2)$
∴$s^2_$甲$=s^2_$乙
解析:
(1)$\overline{x}_{甲}=\frac{48+52+47+49+54}{5}=50$,$\overline{x}_{乙}=\frac{-2+2-3-1+4}{5}=0$,$\overline{x}_{甲}=50+\overline{x}_{乙}$;
(2)$s^{2}_{甲}=\frac{(48-50)^{2}+(52-50)^{2}+(47-50)^{2}+(49-50)^{2}+(54-50)^{2}}{5}=6.8$,$s^{2}_{乙}=\frac{(-2-0)^{2}+(2-0)^{2}+(-3-0)^{2}+(-1-0)^{2}+(4-0)^{2}}{5}=6.8$,$s^{2}_{甲}=s^{2}_{乙}$。