1. 若点M到△ABC的边BC两端点的距离相等,则点M在(
D
)
A.BC的中线上
B.BC的高上
C.AB的垂直平分线上
D.BC的垂直平分线上
答案:D
解析:
根据线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等。反之,到线段两端点距离相等的点在线段的垂直平分线上。因为点M到△ABC的边BC两端点的距离相等,所以点M在BC的垂直平分线上。
2. 下列说法中正确的是(
A
)
A.关于某直线对称的两个三角形是全等三角形
B.两个全等的三角形是关于某直线对称的
C.若两个图形关于某直线对称,则这两个图形一定分别位于该直线的两侧
D.若点A,B关于直线MN对称,则AB垂直平分MN
答案:A
解析:
A. 关于某直线对称的两个三角形是全等三角形。这是正确的,因为如果两个三角形关于某条直线对称,则它们的所有对应边和对应角都相等,满足全等三角形的条件。
B. 两个全等的三角形是关于某直线对称的。这是错误的,因为两个全等三角形不一定关于某条直线对称,它们可能通过平移、旋转等得到,而不仅仅是通过轴对称。
C. 若两个图形关于某直线对称,则这两个图形一定分别位于该直线的两侧。这是错误的,因为两个图形也可能与该直线相交,一部分在一侧,另一部分在另一侧,或者与直线有部分重合。
D. 若点A,B关于直线MN对称,则AB垂直平分MN。这是错误的,应该是直线MN垂直平分线段AB,而不是AB垂直平分MN。
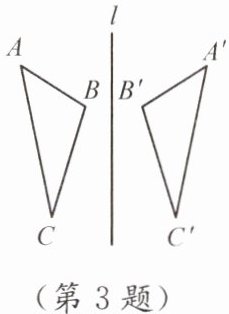
3. 如图,△ABC与△A'B'C'关于直线l对称,且∠A= 50°,∠C'= 30°,则∠B的度数为
100°
.
答案:100°
解析:
由于△ABC与△A'B'C'关于直线l对称,因此它们的对应角相等,即∠C = ∠C'。
已知∠C' = 30°,所以∠C = 30°。
在△ABC中,内角和为180°,即∠A + ∠B + ∠C = 180°。
已知∠A = 50°,∠C = 30°,代入得:
50° + ∠B + 30° = 180°。
解此方程得:
∠B = 180° - 50° - 30° = 100°。
4. 笔直的河岸l旁有A,B两个货场,现要把A货场的货物运往B货场,按计划要先到河岸M处再接一批货物,然后一起运到B货场.
(1)如图①,当A,B货场在河岸l两侧时,要使运输总路程最短,点M应选在河岸l的什么位置?请在图①中作图,并说明理由.
(2)如图②,当A,B货场在河岸l同侧时,要使运输总路程最短,点M应选在河岸l的什么位置?请在图②中作图,并说明理由.

答案:(1) 作图:连接AB,交直线l于点M。
理由:两点之间线段最短,此时AM+MB=AB为最短路径。
(2) 作图:作点A关于直线l的对称点A',连接A'B交直线l于点M。
理由:轴对称性质得AM=A'M,故AM+MB=A'M+MB=A'B,两点之间线段最短,此时总路程最短。