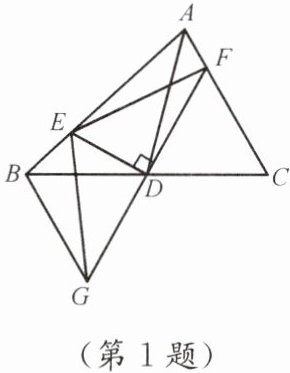
1. 如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,作DE⊥GF,交AB于点E,连接EG.
(1)求证:BG= CF.
(2)判断BE+CF与EF的大小关系,并证明.
答案:(1)证明:∵D是BC的中点,∴BD=CD.
∵BG//AC,∴∠GBD=∠FCD(两直线平行,内错角相等).
在△BDG和△CDF中,
∠GBD=∠FCD,
BD=CD,
∠BDG=∠CDF(对顶角相等),
∴△BDG≌△CDF(ASA),
∴BG=CF.
(2)BE+CF>EF.
证明:由(1)知BG=CF,△BDG≌△CDF,∴DG=DF,即D为GF中点.
∵DE⊥GF,∴DE垂直平分GF,
∴EG=EF(线段垂直平分线上的点到线段两端点距离相等).
在△BEG中,BE+BG>EG(三角形两边之和大于第三边),
∵BG=CF,EG=EF,∴BE+CF>EF.
2. 如图,小宇在一次手工制作活动中,先把一张长方形纸片按图①的方式进行折叠,使折痕的左侧部分比右侧部分短1 cm;展开后按图②的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1 cm,将纸片展开,此时两条折痕之间的距离是
1
cm.

答案:1
解析:
设长方形纸片的长度为 $ L \, cm $。
第一次折叠:折痕左侧部分比右侧部分短 $ 1 \, cm $,设左侧长 $ a $,右侧长 $ b $,则 $ a = b - 1 $,且 $ a + b = L $。解得 $ a = \frac{L - 1}{2} $,故第一次折痕距离左侧边缘 $ \frac{L - 1}{2} \, cm $。
第二次折叠:折痕左侧部分比右侧部分长 $ 1 \, cm $,设左侧长 $ c $,右侧长 $ d $,则 $ c = d + 1 $,且 $ c + d = L $。解得 $ c = \frac{L + 1}{2} $,故第二次折痕距离左侧边缘 $ \frac{L + 1}{2} \, cm $。
两条折痕距离:$ \frac{L + 1}{2} - \frac{L - 1}{2} = 1 \, cm $。