1. 如图,已知AC⊥BD,垂足为O,AO= CO,AB= CD,由此可得△AOB≌△COD,理由是(
A
)
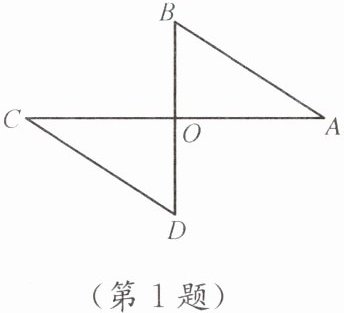
A.HL
B.SAS
C.ASA
D.AAS
答案:A
解析:
因为$AC\perp BD$,所以在$\triangle AOB$和$\triangle COD$中,$\angle AOB = \angle COD=90^{\circ}$。
已知$AO = CO$,$AB = CD$。
在直角三角形中,一条直角边和斜边对应相等的两个直角三角形全等($HL$定理),在$Rt\triangle AOB$和$Rt\triangle COD$中,$AO$、$CO$是直角边,$AB$、$CD$是斜边,满足$HL$定理的条件。
2. 下列选项中,不能判定两个直角三角形全等的是(
B
)
A.斜边和一条直角边分别相等
B.两个锐角分别相等
C.一个锐角和斜边分别相等
D.两条直角边分别相等
答案:B
解析:
A选项根据HL(斜边和一条直角边对应相等的两个直角三角形全等)可判定两个直角三角形全等;C选项根据AAS(两角及其中一角的对边对应相等的两个三角形全等)可判定两个直角三角形全等;D选项根据SAS(两边及其夹角对应相等的两个三角形全等)可判定两个直角三角形全等;而B选项中两个锐角分别相等,只能说明两个直角三角形相似,不能判定全等。
3. 如图,在△ABC中,AB= CB,∠ABC= 90°. D为AB延长线上的一点,点E在边BC上,连接AE,DE,DC,AE= CD. 求证:∠BAE= ∠BCD.

答案:∵∠ABC=90°,D为AB延长线上一点,
∴∠ABE=∠CBD=90°。
在Rt△ABE和Rt△CBD中,
∵AB=CB,AE=CD,
∴Rt△ABE≌Rt△CBD(HL)。
∴∠BAE=∠BCD。
4. 如图,AB= AE,BC= ED,∠B= ∠E,AF⊥CD,垂足为F. 求证:F是CD的中点.

答案:连接AC、AD。
在△ABC和△AED中,
∵AB=AE,∠B=∠E,BC=ED,
∴△ABC≌△AED(SAS),
∴AC=AD。
∵AF⊥CD,
∴∠AFC=∠AFD=90°。
在Rt△AFC和Rt△AFD中,
∵AC=AD,AF=AF,
∴Rt△AFC≌Rt△AFD(HL),
∴CF=DF,
即F是CD的中点。