10. (10分)在正方形网格图①、图②中各画一个等腰三角形.
要求:每个等腰三角形的一个顶点为格点A,其余顶点从格点B,C,D,E,F,G,H中选取,并且所画的两个三角形不全等.
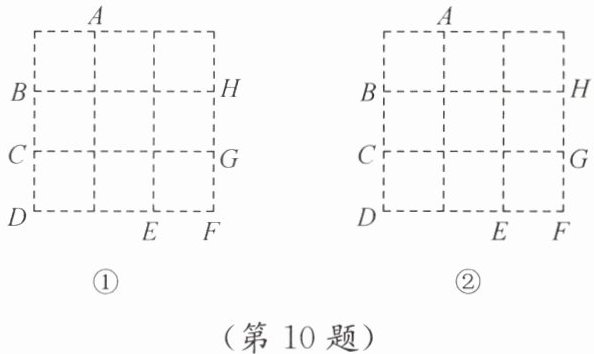
答案:图①:△ABH(顶点A、B、H)
图②:△ACG(顶点A、C、G)
(注:△ABH中AB=AH=1,BH=2;△ACG中AC=AG=√2,CG=2,两三角形不全等)
11. (12分)如图,在△ABC中,AB= AC,DE垂直平分AB,BE⊥AC,AF⊥BC,垂足分别为D,E,F,求∠EFC的度数.

答案:∵DE垂直平分AB,E在DE上,∴EA=EB(垂直平分线性质)。
∵BE⊥AC,∴∠AEB=90°,在Rt△ABE中,EA=EB,∴∠EAB=∠EBA=45°,即∠BAC=45°。
∵AB=AC,∴∠ABC=∠ACB=(180°-45°)/2=67.5°。
∵AF⊥BC,AB=AC,∴F为BC中点(等腰三角形三线合一)。
∵BE⊥AC,∴△BEC为直角三角形,F为BC中点,∴EF=FC(直角三角形斜边中线等于斜边一半)。
在△EFC中,EF=FC,∴∠FEC=∠FCE=∠ACB=67.5°。
∴∠EFC=180°-2×67.5°=45°。
45°
12. (14分)如图,在△ABC中,∠ABE= 2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E.
(1) 若∠C= 30°,求证:AB= 2BE.
(2) 若∠C≠30°,求证:BE= $\frac{1}{2}$(AC-AB).

答案:(1)证明:∵∠C=30°,∠ABE=2∠C,∴∠ABE=60°.
∵BE⊥AD,∴∠AEB=90°.
在Rt△ABE中,∠BAE=90°-∠ABE=30°,
∴BE=1/2AB(直角三角形中30°角所对直角边是斜边的一半),
∴AB=2BE.
(2)证明:延长BE交AC于点F.
∵AD平分∠BAC,∴∠BAE=∠FAE.
∵BE⊥AD,∴∠AEB=∠AEF=90°.
在△AEB和△AEF中,
∠BAE=∠FAE,AE=AE,∠AEB=∠AEF,
∴△AEB≌△AEF(ASA).
∴AB=AF,BE=EF,∠ABF=∠AFB.
∵∠ABF=2∠C,∴∠AFB=2∠C.
∵∠AFB是△BFC的外角,∴∠AFB=∠FBC+∠C.
∴2∠C=∠FBC+∠C,∴∠FBC=∠C.
∴BF=FC(等角对等边).
∵BF=BE+EF=2BE,FC=AC-AF=AC-AB,
∴2BE=AC-AB,
∴BE=1/2(AC-AB).
13. (14分)(1) 如图①,∠C= 90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但需保留作图痕迹).
(2) 已知内角大小的两个三角形如图②、图③所示.能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的大小.

答案:(1) 作图痕迹如下:以点C为顶点,利用圆规和直尺作∠ACD=∠A=24°,射线CD交AB于点D,直线CD即为所求(作图痕迹保留)。
(2) 图②能分割,两个等腰三角形顶角分别为132°和84°;图③不能分割。