1. 选择题:
(1)一次函数$y = 2x - 3$的图象不经过(
B
)
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
(2)下列一次函数中,函数值$y随自变量x$的增大而增大的是(
D
)
A. $y= -5x + 3$
B. $y= -x + 7$
C. $y = 9-2x$
D. $y= x + 3$
答案:[解析]:
本题可根据一次函数的性质来分别求解两个选择题。
(1)判断一次函数$y = 2x - 3$的图象不经过的象限
对于一次函数$y=kx+b$($k$,$b$为常数,$k\neq0$),根据$k$、$b$的正负来确定函数图象经过的象限:
当$k\gt0$,$b\gt0$时,函数图象经过一、二、三象限;
当$k\gt0$,$b\lt0$时,函数图象经过一、三、四象限;
当$k\lt0$,$b\gt0$时,函数图象经过一、二、四象限;
当$k\lt0$,$b\lt0$时,函数图象经过二、三、四象限。
在一次函数$y = 2x - 3$中,$k = 2\gt 0$,$b = -3\lt 0$,所以该函数图象经过一、三、四象限,不经过第二象限。
(2)判断函数值$y$随自变量$x$的增大而增大的一次函数
对于一次函数$y=kx+b$($k$,$b$为常数,$k\neq0$),当$k\gt0$时,$y$随$x$的增大而增大;当$k\lt0$时,$y$随$x$的增大而减小。
选项A:$y = -5x + 3$中,$k = -5\lt 0$,所以$y$随$x$的增大而减小,不符合要求。
选项B:$y = -x + 7$中,$k = -1\lt 0$,所以$y$随$x$的增大而减小,不符合要求。
选项C:$y = 9 - 2x$可变形为$y=-2x + 9$,其中$k = -2\lt 0$,所以$y$随$x$的增大而减小,不符合要求。
选项D:$y = x + 3$中,$k = 1\gt 0$,所以$y$随$x$的增大而增大,符合要求。
[答案]:
(1)B
(2)D
2. 填空题:
(1)已知函数$y= (m + 1)x^{|m|-3}+3$是一次函数,且$y随x$的增大而减小,则$m= $
-4
.
(2)已知一次函数$y= -\dfrac{x}{5}+3的图象与y = kx + 1$的图象互相平行,则$k= $
$-\dfrac{1}{5}$
.
(3)一次函数的图象过点$(0,2)$,且函数值$y随自变量x$的增大而增大,请写出一个符合条件的函数表达式:
$y = x + 2$(答案不唯一)
.
(4)若点$(a,b)$在第二象限,则一次函数$y = ax + b$的图象不经过第
三
象限.
答案:
(1) -4
(2) $-\dfrac{1}{5}$
(3) $y = x + 2$(答案不唯一)
(4) 三
解析:
(1) 函数为一次函数,故指数$|m| - 3 = 1$,解得$|m| = 4$,即$m = 4$或$m = -4$。
又因$y$随$x$增大而减小,需斜率$m + 1 < 0$,即$m < -1$,故$m = -4$。
(2) 两直线平行则斜率相等。已知$y = -\dfrac{x}{5} + 3$的斜率为$-\dfrac{1}{5}$,故$k = -\dfrac{1}{5}$。
(3) 设一次函数为$y = kx + 2$(过点$(0,2)$),因$y$随$x$增大而增大,需$k > 0$。取$k = 1$,则表达式为$y = x + 2$。
(4) 点$(a,b)$在第二象限,故$a < 0$,$b > 0$。函数$y = ax + b$的斜率为负,截距为正,图象经过第二、一、四象限,不经过第三象限。
1. 若点$(-4,y_{1})$,$(2,y_{2})都在一次函数y= -\dfrac{1}{3}x + t$的图象上,则$y_{1}与y_{2}$的大小关系是(
A
)
A.$y_{1}>y_{2}$
B.$y_{1}= y_{2}$
C.$y_{1}<y_{2}$
D.无法确定
答案:A
解析:
一次函数$y = -\dfrac{1}{3}x + t$的斜率$k = -\dfrac{1}{3} < 0$,说明函数单调递减。当$x$增大时,$y$减小。
点$(-4, y_1)$和$(2, y_2)$代入函数:
$y_1 = -\dfrac{1}{3} × (-4) + t = \dfrac{4}{3} + t$
$y_2 = -\dfrac{1}{3} × 2 + t = -\dfrac{2}{3} + t$
比较$y_1$和$y_2$:
$\dfrac{4}{3} + t > -\dfrac{2}{3} + t$,即$y_1 > y_2$。
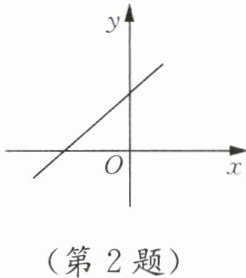
2. 已知一次函数$y = mx + n-2$的图象如图所示,则$m$,$n$的取值范围是(
A
)
A.$m>0$,$n<2$
B.$m<0$,$n<2$
C.$m>0$,$n>2$
D.$m<0$,$n>2$
答案:A
解析:
根据图象是一次函数$y=mx+n-2$的图象是一条上升的直线,且与$y$轴的交点在负半轴上,
因为一次函数$y=kx+b$,$k>0$,函数图象单调递增,$k<0$,函数图象单调递减,$b>0$,图象与$y$轴交于正半轴,$b<0$,图象与$y$轴交于负半轴,
所以可得$m>0$,$n-2<0$,
解得$m>0$,$n<2$。
3. 已知一次函数$y = 3x - b$,它的图象与坐标轴所围成的图形的面积等于6,则$b$的值为
±6
.
答案:±6
解析:
1. 首先,求一次函数$y = 3x - b$与$x$轴和$y$轴的交点。
当$x = 0$时,$y = -b$,所以与$y$轴的交点为$(0, -b)$。
当$y = 0$时,$3x - b = 0$,解得$x = \frac{b}{3}$,所以与$x$轴的交点为$\left(\frac{b}{3}, 0\right)$。
2. 接着,计算该函数图象与坐标轴围成的三角形面积。
三角形的底为$|-b|$,高为$\left|\frac{b}{3}\right|$。
根据三角形面积公式$S = \frac{1}{2} × 底 × 高$,可得$S = \frac{1}{2} × |-b| × \left|\frac{b}{3}\right| = \frac{1}{6}b^{2}$。
3. 最后,根据题目条件求解$b$。
已知面积$S = 6$,则$\frac{1}{6}b^{2} = 6$。
两边同时乘以$6$,得到$b^{2} = 36$。
解得$b = \pm 6$。
4. 已知一次函数$y = kx + 4的图象经过点(-3,-2)$.
(1)求这个函数的表达式;
(2)建立适当的平面直角坐标系,画出该函数的图象;
(3)判断点$(-5,3)$是否在此函数的图象上;
(4)写出把这条直线向下平移4个单位长度后相应的函数表达式.
答案:(1)因为一次函数$y = kx + 4$经过点$(-3, -2)$,可以将这个点代入方程中,得到$-2 = -3k + 4$,解得$k = 2$,因此,这个函数的表达式为$y = 2x + 4$。
(2)为了画出该函数的图象,可以选择两个点,例如$(0, 4)$和$(-2, 0)$,在平面直角坐标系中标出这两个点,然后用直线连接,得到函数$y = 2x + 4$的图象。
(3)判断点$(-5, 3)$是否在此函数的图象上可以将这个点代入函数表达式$y = 2x + 4$中,得到$y = 2 × (-5) + 4 = -6$,这与给定的$y$值$3$不相等,因此点$(-5, 3)$不在此函数的图象上。
(4)把这条直线向下平移$4$个单位长度后相应的函数表达式为$y = 2x$。
解析:
(1)将点$(-3,-2)$代入$y = kx + 4$,得$-2=-3k + 4$,解得$k = 2$,函数表达式为$y=2x + 4$。
(2)列表:
| $x$ | $0$ | $-2$ |
| --- | --- | --- |
| $y$ | $4$ | $0$ |
描点$(0,4)$,$(-2,0)$,连线得函数图象。
(3)当$x=-5$时,$y=2×(-5)+4=-6\neq3$,点$(-5,3)$不在此函数图象上。
(4)$y=2x + 4-4=2x$