活动一:看一看 想一想
阅读课本第 156 页的"问题"、第 157 页的"讨论",回答下列问题:
(1)你能否找出影响一次函数图象从左向右变化趋势(上升或下降)的因素,并结合表达式给出合理解释?
(2)根据图象的变化趋势,你觉得应该怎样描述$y随x$的变化规律?
(3)一次函数$y = kx + b图象与y$轴的交点坐标是什么?$b对一次函数y = kx + b图象与y$轴交点位置有什么影响?
答案:(1)斜率$k$;(2)当$k>0$时,$y$随$x$的增大而增大;当$k<0$时,$y$随$x$的增大而减小;(3)$(0,b)$,$b$决定交点在$y$轴上的位置。
解析:
(1)一次函数的一般形式为$y=kx+b$,其中$k$为斜率。当$k>0$时,函数的图像从左向右看是上升的,表示$y$随$x$的增大而增大;当$k<0$时,函数的图像从左向右看是下降的,表示$y$随$x$的增大而减小。因此,斜率$k$是影响一次函数图象从左向右变化趋势(上升或下降)的关键因素。
(2)根据图象的变化趋势,我们可以这样描述$y$随$x$的变化规律:当斜率$k>0$时,$y$随$x$的增大而增大,函数图像是上升的;当斜率$k<0$时,$y$随$x$的增大而减小,函数图像是下降的。
(3)对于一次函数$y=kx+b$,当$x=0$时,$y=b$。因此,一次函数$y=kx+b$的图象与$y$轴的交点坐标是$(0,b)$。参数$b$决定了函数图象与$y$轴的交点位置,$b$的值就是交点$y$坐标的值。
活动二:想一想 做一做
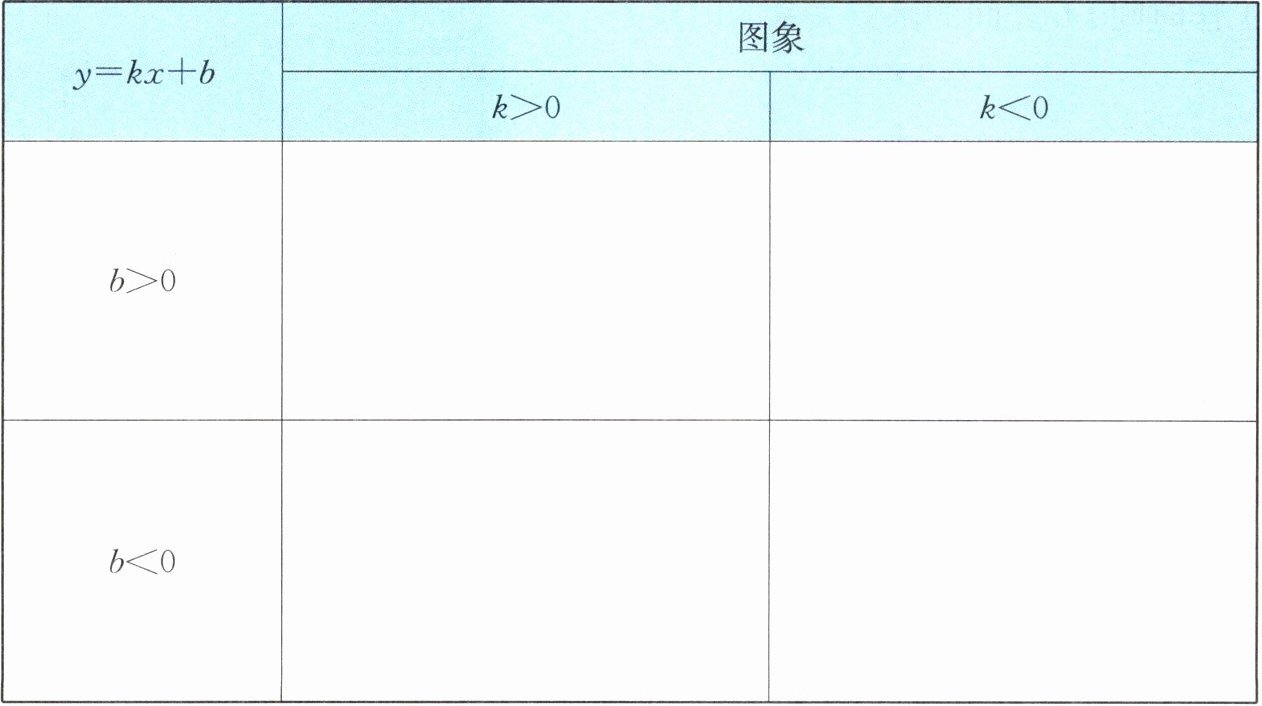
一次函数$y = kx + b的图象经过的象限与k$,$b$的符号的关系:
(1)$k>0$,$b>0\Leftrightarrow y = kx + b$的图象经过
一、二、三
象限;
(2)$k>0$,$b<0\Leftrightarrow y = kx + b$的图象经过
一、三、四
象限;
(3)$k<0$,$b>0\Leftrightarrow y = kx + b$的图象经过
一、二、四
象限;
(4)$k<0$,$b<0\Leftrightarrow y = kx + b$的图象经过
二、三、四
象限.
答案:
(1) 一、二、三
(2) 一、三、四
(3) 一、二、四
(4) 二、三、四
解析:
(1) 当$k\gt0$时,直线从左到右是上升的,$b\gt0$表示直线与$y$轴交于正半轴,所以$y = kx + b$的图象经过一、二、三象限。
(2) 当$k\gt0$时,直线从左到右上升,$b\lt0$表示直线与$y$轴交于负半轴,所以$y = kx + b$的图象经过一、三、四象限。
(3) 当$k\lt0$时,直线从左到右是下降的,$b\gt0$表示直线与$y$轴交于正半轴,所以$y = kx + b$的图象经过一、二、四象限。
(4) 当$k\lt0$时,直线从左到右下降,$b\lt0$表示直线与$y$轴交于负半轴,所以$y = kx + b$的图象经过二、三、四象限。