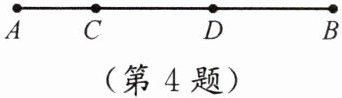
4. 如图,AC= 2,BD= 3,D是线段BC的中点.求线段AB的长.
答案:
解:∵D是BC中点,∴DC=DB
∴AB=AC+BC=AC+2BD=8
5. 如图,点C,D,E都在线段AB上,已知AD= BC,E是线段AB的中点,那么E是线段CD的中点吗?请说明理由.

答案:解:是,理由:
∵AD=BC,即AC+CD=BD+CD
∴AC=BD
∵E是AB中点,∴AE=BE
∴AC+CE=BD+DE
∴CE=AE-AC,DE=BE-BD
又∵AE=BE,AC=BD
∴CE=DE,即E为CD中点
1. 如图,点A,B,C,D在直线l上,且AC= 5,BD= 4,则AB-CD=
1
.
答案:1
解析:
由图可知,$AC=AB+BC=5$,$BD=BC+CD=4$。
$AB - CD = (AB + BC) - (BC + CD) = AC - BD = 5 - 4 = 1$
1
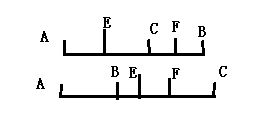
2. 已知线段AC和BC在一条直线上,AC= 5,BC= 3.画出图形并求线段AC的中点和线段BC的中点之间的距离.
答案:解:如图,E为AC中点,F为BC中点
①:当C在AB之间时$,EF=EC+CF=\frac {1}{2}AC+\frac {1}{2}CB=4$
②:当B在AC之间时$,EF=EC-CF=\frac {1}{2}AC-\frac {1}{2}CB=1$
综上,它们距离为1或4
解析:
情况一:点B在线段AC上
设AC中点为M,BC中点为N。
$ AM = \frac{1}{2}AC = \frac{5}{2} $,$ BN = \frac{1}{2}BC = \frac{3}{2} $。
$ MN = AC - AM - CN = 5 - \frac{5}{2} - \frac{3}{2} = 1 $。
情况二:点B在线段AC延长线上
设AC中点为M,BC中点为N。
$ AM = \frac{1}{2}AC = \frac{5}{2} $,$ CN = \frac{1}{2}BC = \frac{3}{2} $。
$ MN = MC + CN = \frac{5}{2} + \frac{3}{2} = 4 $。
结论:中点之间的距离为1或4。
3. (1)如图①,线段AB= 12,C是线段AB的中点,D,E分别是线段AC,BC的中点,则DE=
6
.
请对照图形,完成下列解答过程.

解:因为C是线段AB的中点,且AB= 12,
所以
AC
=
BC
= $\frac{1}{2}$AB= 6.
因为D,E分别是线段AC,BC的中点,
所以
DC
= $\frac{1}{2}$AC= 3,
CE
= $\frac{1}{2}$BC= 3,
所以DE=
DC
+
CE
= 6.
(2)将上述问题中的“C是线段AB的中点”改为“C是线段AB上的任意一点”(图②),其他条件不变,则DE=
6
.请仿照(1)写出解题过程.
(2)解:∵D,E分别是线段AC,BC中点
∴$DC=\frac {1}{2}AC,CE=\frac {1}{2}CB$
∴$DE=DC+CE=\frac {1}{2}(AC+CB)=\frac {1}{2}AB=6$
(3)如图③,如果C,D是线段AB上的任意两点,E,F分别是线段AC,BD的中点,且线段EF= m,线段CD= n,则AB=
2m-n
(直接写出结果).
答案:6
AC
BC
DC
CE
DC
CE
6
2m-n
(2)解:∵D,E分别是线段AC,BC中点
∴$DC=\frac {1}{2}AC,CE=\frac {1}{2}CB$
∴$DE=DC+CE=\frac {1}{2}(AC+CB)=\frac {1}{2}AB=6$
解析:
(1)因为C是线段AB的中点,且AB= 12,
所以AC= BC= $\frac{1}{2}$AB= 6。
因为D,E分别是线段AC,BC的中点,
所以DC= $\frac{1}{2}$AC= 3,CE= $\frac{1}{2}$BC= 3,
所以DE= DC+CE= 6。
(2)因为AB= 12,C是线段AB上的任意一点,
所以AC+BC= AB= 12。
因为D,E分别是线段AC,BC的中点,
所以$DC=\frac{1}{2}AC$,$CE= \frac{1}{2}BC$,
所以$DE=DC+CE=\frac{1}{2}AC+\frac{1}{2}BC=\frac{1}{2}(AC+BC)=\frac{1}{2}×12 = 6$。
(3)因为E,F分别是线段AC,BD的中点,
所以$AC=2CE$,$BD=2DF$。
又因为$EF=m$,$CD=n$,
所以$AB=AC+BD-CD=2CE+2DF-CD=2(CE+DF-CD)+CD=2(EF-CD)+CD=2(m-n)+n=2m-n$。