1. 填空:
(1)$(-2)^{6}$读作
(-2)的6次方
,表示
6个(-2)相乘
,其中指数为
6
,底数为
-2
;
(2)$-2^{6}$读作
2的6次方的相反数
,表示
6个2相乘的积的相反数
,其中指数为
6
,底数为
2
.
答案:(-2)的6次方
6个(-2)相乘
6
-2
2的6次方的相反数
6个2相乘的
积的相反数
6
2
解析:
(1) 对于$(-2)^{6}$,它表示$-2$自乘6次。因此,它读作“负2的6次方”,表示6个$-2$相乘,其中指数为6,底数为$-2$。
(2) 对于$-2^{6}$,它表示$2$自乘6次后再取其相反数。因此,它读作“2的6次方的相反数”,表示6个2相乘的相反数,其中指数为6,底数为2。
2. $\frac{49}{121}= $
$±\frac{7}{11}$
$^{2}$,$(-2×4)^{3}= $
-512
.
答案:$±\frac{7}{11}$
-512
解析:
对于 $\frac{49}{121}= (\quad)^{2}$,我们需要找到一个数,使其平方等于 $\frac{49}{121}$。
由于 $(\frac{7}{11})^{2} = \frac{49}{121}$,所以第一个空应填 $\pm\frac{7}{11}$。
对于$(-2×4)^{3}$,首先计算括号内的乘法,得到 $-8$,然后对 $-8$ 进行三次方运算,即 $(-8)^{3} = -512$。
3. 下列各组数中,运算结果相同的是(
C
)
A.$3^{4}和4^{3}$
B.$-3^{2}和(-3)^{2}$
C.$(-2)^{3}和-2^{3}$
D.$(-\frac{2}{3})^{2}和(-\frac{3}{2})^{2}$
答案:C
解析:
A.$3^{4}=81$,$4^{3}=64$,$81\neq64$
B.$-3^{2}=-9$,$(-3)^{2}=9$,$-9\neq9$
C.$(-2)^{3}=-8$,$-2^{3}=-8$,$-8=-8$
D.$(-\frac{2}{3})^{2}=\frac{4}{9}$,$(-\frac{3}{2})^{2}=\frac{9}{4}$,$\frac{4}{9}\neq\frac{9}{4}$
C
4. 下列说法中,正确的有(
B
)
① 对于任意有理数m,都有$m^{2}>0$;② 对于任意有理数m,都有$m^{2}= (-m)^{2}$;③ 对于任意有理数m,n(m≠n),都有$(m-n)^{2}>0$;④ 对于任意有理数m,都有$m^{3}= (-m)^{3}$.
A.1个
B.2个
C.3个
D.0个
答案:B
解析:
① 当$m=0$时,$m^{2}=0$,故①错误;
② 因为$(-m)^{2}=m^{2}$,所以对于任意有理数$m$,都有$m^{2}=(-m)^{2}$,故②正确;
③ 因为$m≠n$,所以$m - n≠0$,则$(m - n)^{2}>0$,故③正确;
④ 当$m=1$时,$m^{3}=1$,$(-m)^{3}=-1$,$1≠-1$,故④错误。
正确的有②③,共2个。
B
5. 计算:(1)$(-5)^{2}$; (2)$(-0.1)^{4}$; (3)$(-\frac{2}{3})^{3}$; (4)$(-\frac{1}{5})^{3}$.
答案:解:原式=0.0001
解:原式$=-\frac{8}{27}$
解:原式$=-\frac{1}{125}\ $
解:原式=25
1. 下列算式中,结果为正数的是(
B
)
A.$-(-4)^{2}$
B.$-(-4^{2})$
C.$-|-4|^{2}$
D.$-[-(-4)]$
答案:B
解析:
A.$-(-4)^{2}=-16$
B.$-(-4^{2})=16$
C.$-|-4|^{2}=-16$
D.$-[-(-4)]=-4$
结果为正数的是B。
2. 观察下列数据,按规律在横线上填写适当的数:
1,$-\frac{3}{4}$,$\frac{5}{9}$,$-\frac{7}{16}$,$\frac{9}{25}$,
$-\frac{11}{36}$
,…
答案:$-\frac{11}{36}$
解析:
观察数列1,$-\frac{3}{4}$,$\frac{5}{9}$,$-\frac{7}{16}$,$\frac{9}{25}$,可以发现数列的每一项的绝对值部分符合$\frac{2n-1}{n^2}$的规律,其中$n$为项数。同时,数列的符号交替出现,即正负相间。
对于第6项,其绝对值部分应为$\frac{2×6-1}{6^2}=\frac{11}{36}$,符号为负(因为第5项为正,所以第6项为负)。
所以,第6项为$-\frac{11}{36}$。
3. 用“<”将$\frac{1}{4}$,0,$-\frac{2}{3}$,$(-\frac{1}{5})^{2}$,$(-3)^{3}$按从小到大的顺序排列:
$(-3)^{3},-\frac{2}{3},0,(-\frac{1}{5})^{2},\frac{1}{4}$
.
答案:$(-3)^{3},-\frac{2}{3},0,(-\frac{1}{5})^{2},\frac{1}{4}$
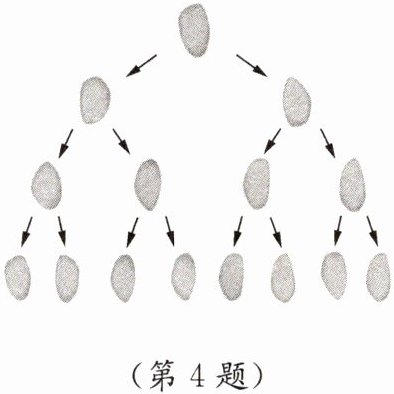
4. 细菌通过分裂的方式进行繁殖,1个细菌分裂成2个细菌,这2个细菌又分别能分裂成2个细菌……如图是某种细菌分裂的示意图,已知该种细菌每20 min能分裂一次,则1个该种细菌经过3 h可以分裂成
512
个细菌.
答案:512