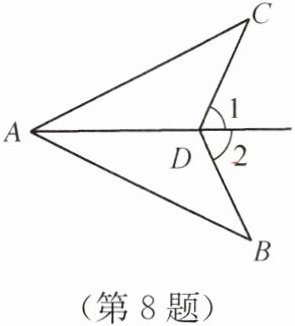
8. 如图,∠1= ∠2,BD= CD. 求证:AD是∠BAC的平分线.
答案:
∵$∠1 = ∠2,$
∴$∠ADC = ∠ADB.$
∴在$△ABD$和$△ACD$中,
$BD = CD,∠BDA = ∠CDA,AD = AD,$
∴$△ABD≌△ACD(SAS).$
∴$∠CAD = ∠BAD,$
∴$AD$是$∠BAC$的平分线
9. 如图,AB= AD,AC= AE,∠BAE= ∠DAC. 求证:∠E= ∠C.

答案:
∵$∠BAE = ∠DAC,$
∴$∠BAE + ∠EAC = ∠DAC + ∠EAC,$即$∠BAC = ∠DAE.$
在$△BAC$和$△DAE$中,
$AB = AD,$
$∠BAC = ∠DAE$
$AC = AE$
∴$△BAC≌△DAE(SAS).$
∴$∠E = ∠C$
10. 如图,点C,E,F,A共线,BF= DE,AE= CF,BF//DE.
(1)求证:∠B= ∠D;
(2)试说明AB与CD的关系

答案:1. (1)证明:
因为$AE = CF$,所以$AE+EF = CF + EF$(等式的性质),即$AF = CE$。
又因为$BF// DE$,所以$\angle AFB=\angle CED$(两直线平行,内错角相等)。
在$\triangle ABF$和$\triangle CDE$中,$\left\{\begin{array}{l}BF = DE\\\angle AFB=\angle CED\\AF = CE\end{array}\right.$。
根据$SAS$(边角边)判定定理,可得$\triangle ABF\cong\triangle CDE$。
所以$\angle B=\angle D$(全等三角形的对应角相等)。
2. (2)解:
由(1)知$\triangle ABF\cong\triangle CDE$,所以$AB = CD$(全等三角形的对应边相等),$\angle A=\angle C$(全等三角形的对应角相等)。
因为$\angle A=\angle C$,所以$AB// CD$(内错角相等,两直线平行)。
综上,$AB$与$CD$的关系是$AB = CD$且$AB// CD$。
11. 如图,要测量池塘两岸相对的两点A,B的距离,应如何操作?请你设计一个测量方案.

答案:如图,在 池塘外取一点E,连接AE,BE(AE,BE都在地面上),延长AE,BE分别到点C,D,使CE = AE,DE = BE,连接CD,度量CD的宽度,即可得到AB的长度(理由:△ABE≌△CDE)
