1.
两边
及其
夹角
分别相等的两个三角形全等(简写成“边角边”或“SAS”).
答案:两边,夹角
2. 如图,BD= CD,∠1= ∠2,则△ABD≌
△ACD
.
答案:△ACD
3. 如图,AD= AE,要使△ABE≌△ACD,根据“ SAS”需要添加条件
AC=AB
.
答案:AC=AB
4. 如图,∠DAB= ∠CBA,在△ABD中,AD= 4,BD= 8,要使△ABC≌△BAD,需添加的一个条件是(
D
)
A.AB= 8
B.AC= 8
C.AB= 6
D.CB= 4
答案:D
解析:
在△ABC和△BAD中,已知∠CBA=∠DAB(∠DAB=∠CBA),AB=BA(公共边)。
若添加条件CB=4,因为AD=4,所以CB=AD。
则有:$\left\{\begin{array}{l} CB=AD\\ ∠CBA=∠DAB\\ AB=BA\end{array}\right.$
根据SAS(边角边)全等判定定理,可得△ABC≌△BAD。
D
5. 下列条件中能判定△ABC≌△A'B'C'的是(
D
)
A.AB= A'B',AC= A'C',∠C= ∠C'
B.AB= A'B',∠A= ∠A',BC= B'C'
C.AC= A'C',∠A= ∠A',BC= B'C'
D.AC= A'C',∠C= ∠C',BC= B'C'
答案:D
解析:
选项A:AB=A'B',AC=A'C',∠C=∠C',为SSA,不能判定全等;
选项B:AB=A'B',∠A=∠A',BC=B'C',为SSA,不能判定全等;
选项C:AC=A'C',∠A=∠A',BC=B'C',为SSA,不能判定全等;
选项D:AC=A'C',∠C=∠C',BC=B'C',为SAS,能判定全等。
D
6. 如图,点D在AB上,E为DF,AC的中点,AB= 8,CF= 6,则BD的长为______
2
.
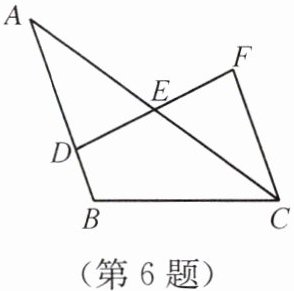
答案:2
解析:
∵E为DF,AC的中点
∴DE=FE,AE=CE
在△AED和△CEF中
$\left\{\begin{array}{l} AE=CE\\ ∠AED=∠CEF\\ DE=FE\end{array}\right.$
∴△AED≌△CEF(SAS)
∴AD=CF=6
∵AB=8
∴BD=AB-AD=8-6=2
2
7. 如图,在△ABC中,AB= AC,AD是△ABC的角平分线. 求证:△ABD≌△ACD.

答案:
∵AD平分∠BAC,
∴∠DAB = ∠DAC.在△ABD和△ACD中,{AB = AC,∠DAB = ∠DAC,AD = AD},
∴△ABD≌△ACD(SAS)