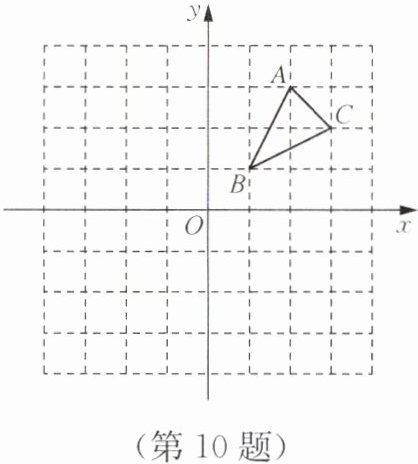
10. 如图,方格纸中的每个小方格都是边长为1的正方形,建立平面直角坐标系后,$△ABC$的顶点都在格点上.
(1)画出$△ABC$关于x轴对称的$△A_1B_1C_1$;
(2)将$△ABC$绕点B按顺时针方向旋转90°得到$△A_2BC_2$,则点$C_2$的坐标为
(2,-1)
;
(3)在y轴上找一点P,使得AP+BP最小,在图中画出点P位置.
作点A(或B)关于y轴的对称点,连接该点与点B(或A),与y轴的交点即为P
答案:(1)略 (2)(2,-1) (3)作点A(或B)关于y轴的对称点,连接该点与点B(或A),与y轴的交点即为P
解析:
(1)(画图略)
(2)$(2,-1)$
(3)(画图略,作法:作点$A$关于$y$轴的对称点$A'$,连接$A'B$,与$y$轴的交点即为点$P$)
11. 在平面直角坐标系中,给出如下定义:点A到x轴、y轴距离的较小值称为点A的“短距”,当点P的“短距”等于点Q的“短距”时,称P,Q两点为“等距点”.
(1)点B(7,-27)的“短距”为
7
;
(2)若点P(5,m-1)的“短距”为3,求m的值;
m=4或-2
(3)若C(-2,k),D(4,3k-5)两点为“等距点”,求k的值.
k=$\frac{7}{3}$或$\frac{5}{4}$
答案:(1)7 (2)m=4或-2 (3)k=$\frac{7}{3}$或$\frac{5}{4}$
解析:
(1)7
(2)由题意得,点P到x轴距离为|m-1|,到y轴距离为5,较小值为3。
因为5>3,所以|m-1|=3,
m-1=3或m-1=-3,
解得m=4或m=-2。
(3)点C到x轴距离为|k|,到y轴距离为2,“短距”为min(|k|,2);
点D到x轴距离为|3k-5|,到y轴距离为4,“短距”为min(|3k-5|,4)。
因为C,D为“等距点”,所以min(|k|,2)=min(|3k-5|,4)。
情况一:|k|≤2且|3k-5|≤4,
则|k|=|3k-5|,
k=3k-5或k=-(3k-5),
解得k=$\frac{5}{2}$或k=$\frac{5}{4}$。
又|k|≤2且|3k-5|≤4,
k=$\frac{5}{2}$时,|k|=$\frac{5}{2}$>2,舍去;k=$\frac{5}{4}$时,|k|=$\frac{5}{4}$≤2,|3k-5|=$\frac{5}{4}$≤4,成立。
情况二:|k|≤2且|3k-5|>4,
则|k|=4,|k|=4与|k|≤2矛盾,无解。
情况三:|k|>2且|3k-5|≤4,
则2=|3k-5|,
3k-5=2或3k-5=-2,
解得k=$\frac{7}{3}$或k=1。
k=1时,|k|=1≤2,舍去;k=$\frac{7}{3}$时,|k|=$\frac{7}{3}$>2,|3k-5|=2≤4,成立。
情况四:|k|>2且|3k-5|>4,
则2=4,不成立。
综上,k=$\frac{7}{3}$或k=$\frac{5}{4}$。
12. 如图①,在平面直角坐标系中,长方形OABC的顶点A,C的坐标分别为(10,0),(0,4),D是OA的中点,点P在边BC上运动,当$△ODP$是腰长为5的等腰三角形时,求点P的坐标.(提示:图②、图③备用,不要漏解)

答案:当OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;当OD是等腰三角形的一条腰时,若O是顶角顶点,点P的坐标是(3,4);若D是顶角顶点,当点P在点M左侧时,点P的坐标是(2,4);当点P在点M右侧时,点P的坐标是(8,4)
解析:
∵长方形OABC中,A(10,0),C(0,4),D是OA中点,
∴OA=10,OC=4,OD=5,点P在BC上,设P(x,4)。
情况1:OD为腰,O为顶角顶点,OP=OD=5。
由勾股定理,$x^2 + 4^2 = 5^2$,解得$x=3$($x=-3$舍),P(3,4)。
情况2:OD为腰,D为顶角顶点,PD=OD=5。
由勾股定理,$(x-5)^2 + 4^2 = 5^2$,解得$x=2$或$x=8$,P(2,4)或(8,4)。
情况3:OD为底边,OP=PD,此时OP≠5,舍去。
综上,点P的坐标为(2,4),(3,4),(8,4)。