10. 如图,在 3×3 的正方形网格中,∠1+∠2=
90°
。
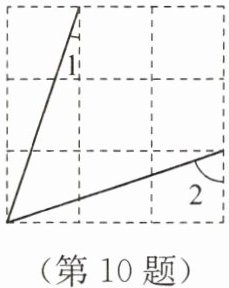
答案:90°
11. 如图,△ADF≌△BCE,BC= 6,DF= 4,△ADF 的周长 l 的取值范围是
12<l<20
。

答案:12<l<20
解析:
∵△ADF≌△BCE,BC=6,DF=4
∴AD=BC=6,AF=BE,CE=DF=4
设AF=BE=x,在△ADF中,AD=6,DF=4,AF=x
根据三角形三边关系:AD - DF < AF < AD + DF
即6 - 4 < x < 6 + 4
2 < x < 10
△ADF的周长l=AD + DF + AF=6 + 4 + x=10 + x
∵2 < x < 10
∴10 + 2 < l < 10 + 10
12 < l < 20
12<l<20
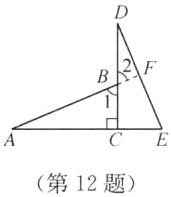
12. 如图,CD⊥AE,垂足为 C,点 B 在 CD 上,△ACB≌△DCE。求证:AB⊥DE。

答案:如图,延长 AB 交 DE 于点 F.
∵ CD⊥AE,
∴ ∠BCA=90°,
∴ ∠1+∠A=90°.
∵ △ACB≌△DCE,
∴ ∠A=∠D.
∵ ∠1=∠2,
∴ ∠D+∠2=∠A+∠1=90°,
∴ ∠DFB=90°,
∴ AF⊥DE,即 AB⊥DE
13. 如图,点 A,D,E 在同一条直线上,△BAD≌△ACE。
(1)BD=
AE
;
(2)当△ABD 满足什么条件时,BD//CE?
当∠ADB=90°时,BD//CE.理由:
∵ △BAD≌△ACE,
∴ ∠ADB=∠AEC.若 BD//CE,则∠BDE=∠AEC,
∴ ∠ADB=∠BDE.
∵ ∠ADB+∠BDE=180°,
∴ ∠ADB=∠BDE=90°
答案:(1)AE (2)当∠ADB=90°时,BD//CE.理由:
∵ △BAD≌△ACE,
∴ ∠ADB=∠AEC.若 BD//CE,则∠BDE=∠AEC,
∴ ∠ADB=∠BDE.
∵ ∠ADB+∠BDE=180°,
∴ ∠ADB=∠BDE=90°
14. 如图,△ABE 和△ADC 是△ABC 分别沿 AB,AC 作轴对称变换得到的,若∠BAC= 150°,求∠DAE,∠BOC 的度数。

答案:∠DAE=90°,∠BOC=120°.如图,
∵ △ABE 和△ABC 成轴对称,△ADC 和△ABC 成轴对称,
∴ △ABE≌△ABC,△ABC≌△ADC,△ABE≌△ADC,
∴ ∠1=∠2=∠ADC,∠BAE=∠BAC=∠DAC=150°,∠3=∠4=∠BEA,
∴ ∠DAE=150°×3-360°=90°.
∵ 在△ABC 中,∠BAC=150°,
∴ ∠2+∠3=180°-∠BAC=30°.
∵ ∠OBC=2∠2,∠OCB=2∠3,
∴ ∠BOC=180°-2×30°=120°
