8. (1)在平面直角坐标系中,将点M(3a-9,1-a)向左平移3个单位长度后落在y轴上,则a=
4
.
(2)在平面直角坐标系中,将点A(5,-8)向上平移得到点B(x+3,x-2),则点B的坐标为
(5,0)
.
答案:
(1) 4
(2) (5,0)
9. 如图,△OAB的顶点A,B的坐标分别为(3,5),(4,0),把△OAB沿x轴向右平移得到△CDE.如果CB=1,那么点D的坐标为
(6,5)
.
答案:(6,5)
解析:
∵B(4,0),△OAB沿x轴向右平移得到△CDE,
∴点C是点O平移后的对应点,设平移距离为a(a>0),则C(a,0)。
∵CB=1,B(4,0),
∴|4 - a|=1,解得a=3或a=5。
由图可知点C在点B左侧,
∴a=3,即平移距离为3个单位长度。
∵A(3,5),
∴点D的坐标为(3+3,5)=(6,5)。
(6,5)
10. 第一象限内有两点P(m-4,n),Q(m,n-3),将线段PQ平移,使点P,Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是
(0,3)或(-4,0)
.
答案:(0,3)或(-4,0)
解析:
设平移向量为$(a,b)$,则点$P(m - 4,n)$平移后的坐标为$(m - 4 + a,n + b)$,点$Q(m,n - 3)$平移后的坐标为$(m + a,n - 3 + b)$。
因为平移后点$P$,$Q$分别落在两条坐标轴上,所以分两种情况:
情况一:点$P$落在$y$轴上,点$Q$落在$x$轴上。
则$\begin{cases}m - 4 + a = 0\\n - 3 + b = 0\end{cases}$,解得$\begin{cases}a = 4 - m\\b = 3 - n\end{cases}$。
此时点$P$平移后的坐标为$(0,n + 3 - n)=(0,3)$。
情况二:点$P$落在$x$轴上,点$Q$落在$y$轴上。
则$\begin{cases}n + b = 0\\m + a = 0\end{cases}$,解得$\begin{cases}b = -n\\a = -m\end{cases}$。
此时点$P$平移后的坐标为$(m - 4 - m,n - n)=(-4,0)$。
综上,点$P$平移后的对应点的坐标是$(0,3)$或$(-4,0)$。
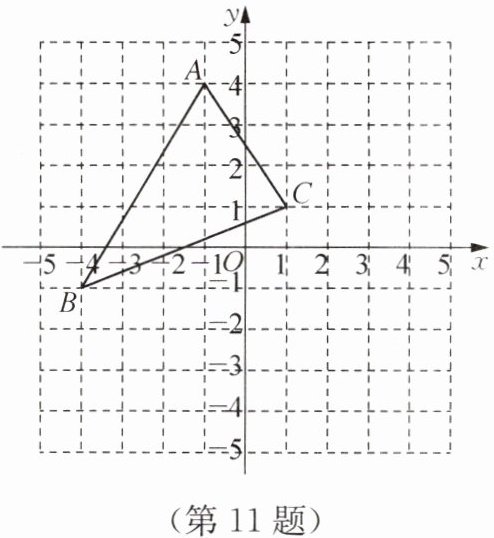
11. 如图,△ABC的顶点坐标分别为A(-1,4),B(-4,-1),C(1,1),将△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A′B′C′,且点C的对应点是C′.
(1)在图中画出△A′B′C′,并直接写出点C′的坐标;
(2)若△ABC内有一点P(a,b),经以上平移后得到对应点P′,直接写出点P′的坐标.
答案:
(1) C'(5,-2)
(2) P'(a+4,b-3)
12. 在平面直角坐标系中,点A,B在第一象限,将线段AB进行平移得到线段CD,点A的对应点为C,点B的对应点为D.
(1)若点A,B,D的坐标分别为(5,8),(3,6),(1,-1),求点C的坐标.
(2)若点A,B,C,D的坐标分别为(m,a),(2,b),(4,c),(2m,-2),△ABC的面积为6,点M在第三象限,横坐标为b-a+2,在x轴上是否存在点P,使得△ABP与△BMD的面积之和等于△AMD的面积?若存在,求点P的坐标;若不存在,请说明理由.
答案:
(1) C(3,1)
(2) P(10,0)或(-6,0) 提示:由平移,可知m=2,a-b=6,得到点M的横坐标为-4.设点P(x,0),根据 S△ABP=S△AMD-S△BMD=S△BAM+△S△ABD,
∴$\frac{1}{2}×6\cdot|x-2|=\frac{1}{2}AB\cdot(x_B-x_M)+\frac{1}{2}AB\cdot(x_D-x_B)$,
∴3|x-2|=$\frac{1}{2}×6×8$,
∴x₁=10,x₂=-6.
∴点P的坐标为(10,0)或(-6,0)