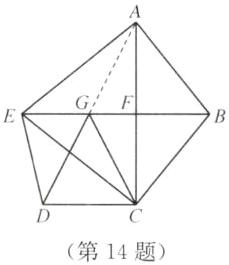
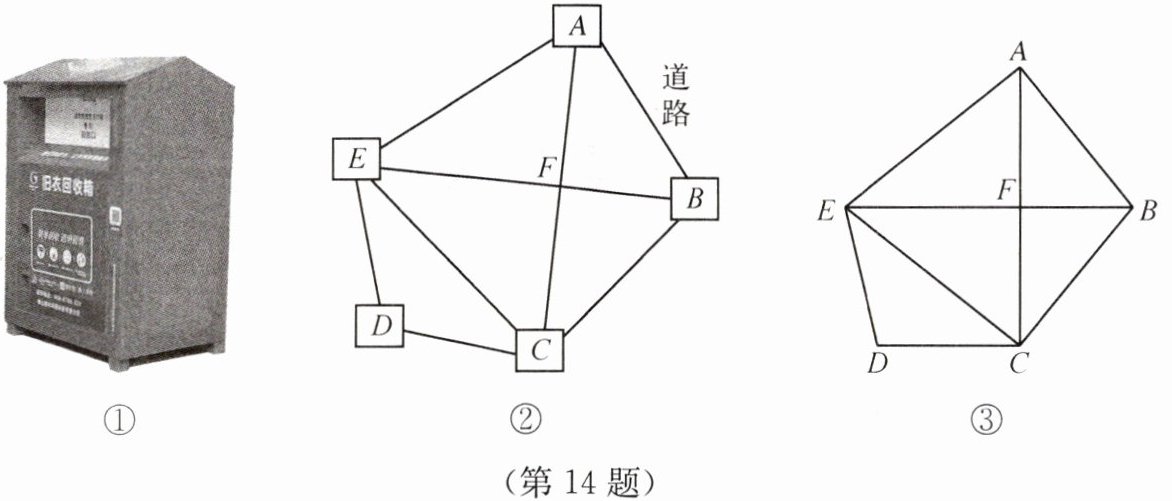
14. 【问题背景】某小区有四栋住宅楼:B栋(B处),C栋(C处),D栋(D处),E栋(E处),A处为小区入口.为方便小区居民传递爱心,物业管理处准备在小区的一条主干道BE上增设一个“爱心衣物回收箱”(图①),现需确定“爱心衣物回收箱”的具体位置,使得它到四栋住宅楼的距离之和最短.某数学兴趣小组成员开展了如下数学活动.
(第14题)
【问题解决】
步骤一:实地测绘.
小组成员借助无人机航测技术绘制了小区平面图(图②),并测量出了某些道路的长度(如下表所示),进一步抽象成几何图形(图③),其中主干道AC与BE交于点F,BE//CD.小组成员又借助电子测角仪测得∠BCE= 90°,∠CEB= ∠CED.
| 道路 | AE | AB | BC | BF | EF | DE |
| 长度/m | 40 | 30 | 30 | 18 | 32 | 25 |

步骤二:数学计算.
根据图③及表格中的相关数据,完成下列计算:
(1)求道路CD的长;
(2)道路AC= ______m;
步骤三:方案设计.
(3)根据以上探究,在主干道BE上画出“爱心衣物回收箱”的具体位置(用点G表示).
(4)“爱心衣物回收箱”到四栋住宅楼的距离之和的最小值为多少米?(结果保留根号)
答案:(1)$\because BE// CD$,$\therefore \angle BEC=\angle DCE$.$\because \angle CEB=\angle CED$,$\therefore \angle CED=\angle DCE$.$\therefore CD=DE=25$,故道路CD的长为25 m (2)48 (3)由(2)可得EB垂直平分AC,根据两点之间线段最短可得AD,EB的交点G到A,E,D,B的距离之和最小,又$GA=GC$,则到四栋距离最小的点即为点G,如图所示 (4)$\because DC// EB$,$EB\perp AC$,$\therefore AC\perp DC$,$\therefore \angle ADC=90^\circ$.$\because$点G在EB上,即AC的垂直平分线上,$\therefore GA=GC$,$\therefore \angle GAC=\angle GCA$.$\because \angle GAC+\angle GCD=90^\circ$,$\angle GCA+\angle GDC=90^\circ$,$\therefore \angle GCD=\angle GDC$.$\therefore GD=GC$,$\therefore GA=GD=GC$,$\therefore CG+DG+EG+BG=AG+GD+EG+GB=AD+EB=\sqrt{DC^2+AC^2}+EB=\sqrt{25^2+48^2}+50=(\sqrt{2929}+50)(m)$