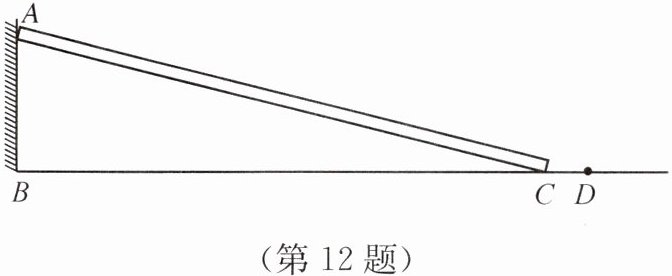
12. 《九章算术》是我国古代数学名著.书中卷九“勾股”中记载:“今有垣高一丈,倚木于垣,上于垣齐.引木却行一尺,其木至地,问木长几何?”其意思是:如图,墙AB高1丈(1丈= 10尺),一根木棒AC靠于墙上,木棒上端与墙头齐平.当木棒下端沿地面从C处向右滑1尺到D处时,木棒上端恰好沿墙壁从A处下滑到墙脚B处(∠ABC= 90°,点B,C,D在同一条水平线上),求木棒的长为多少尺.
答案:设木棒的长为$x$尺,则$BC=(x-1)$尺.在$Rt\triangle ABC$中,由勾股定理,得$AB^2+BC^2=AC^2$,$\therefore 10^2+(x-1)^2=x^2$,解得$x=50.5$,即木棒的长为50.5尺
13. 如图,小巷左右两侧是竖直的墙,已知小巷的宽度CE是2.2 m.一架梯子AB斜靠在左墙时,梯子顶端A距离地面2.4 m.如果保持梯子底端B位置不动,将梯子斜靠在右墙时,梯子顶端D距离地面2 m.求此时梯子底端B到右墙角点E的距离是多少米.

答案:设此时梯子底端B到右墙角点E的距离是$x\ m$,则BC为$(2.2-x)\ m$.由题意可知,$AC=2.4\ m$,$DE=2\ m$,$AB=DB$.在$Rt\triangle ABC$和$Rt\triangle DBE$中,由勾股定理,得$AB^2=BC^2+AC^2$,$DB^2=BE^2+DE^2$,$\therefore BC^2+AC^2=BE^2+DE^2$,即$(2.2-x)^2+2.4^2=x^2+4$,解得$x=1.5$,即此时梯子底端B到右墙角点E的距离是$1.5\ m$