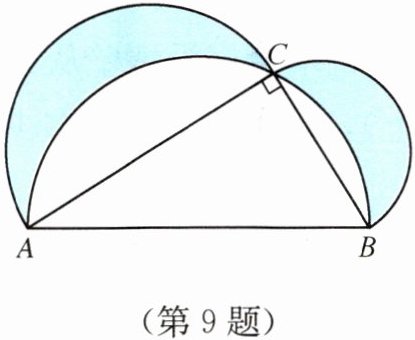
9. 如图,在Rt△ABC中,∠C= 90°,分别以各边为直径向外作半圆,图中的阴影部分在数学史上被称为“希波克拉底月牙”.当AC= 8,BC= 4时,阴影部分的面积为______
16
.
答案:16
解析:
在Rt△ABC中,∠C=90°,AC=8,BC=4。
根据勾股定理,AB²=AC²+BC²=8²+4²=64+16=80。
设以AC为直径的半圆面积为S₁,半径r₁=AC/2=4,S₁=(1/2)πr₁²=(1/2)π×4²=8π。
以BC为直径的半圆面积为S₂,半径r₂=BC/2=2,S₂=(1/2)πr₂²=(1/2)π×2²=2π。
以AB为直径的半圆面积为S₃,半径r₃=AB/2,S₃=(1/2)πr₃²=(1/2)π×(AB²/4)=(1/8)π×80=10π。
Rt△ABC的面积S=(1/2)×AC×BC=(1/2)×8×4=16。
阴影部分面积=S₁+S₂+S - S₃=8π+2π+16 - 10π=16。
16
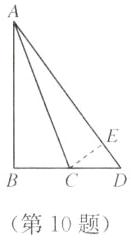
10. 在Rt△ABC中,∠ABC= 90°,D在BC的延长线上,连接AD.
(1)若AC= 13,AB= 12,AD= 15,求CD的长;
(2)若AC平分∠BAD,BC= 9,CD= 15,直接写出AB的长.

答案:(1)在$\triangle ABC$中,$AC=13$,$AB=12$,$\therefore BC=\sqrt{AC^2-AB^2}=5$,在$\triangle ABD$中,$AD=15$,$AB=12$,$\therefore BD=\sqrt{AD^2-AB^2}=9$,$\therefore CD=BD-BC=4$ (2)如图,过点C作$CE\perp AD$,垂足为E,$\because \angle ABC=90^\circ$,AC平分$\angle BAD$,$\therefore CE=BC=9$.在$\triangle CDE$中,$CD=15$,$CE=9$,$\therefore DE=\sqrt{CD^2-CE^2}=12$.在$Rt\triangle ABC$和$Rt\triangle AEC$中,$\left\{\begin{array}{l} AC=AC,\\ BC=EC,\end{array}\right.$ $\therefore Rt\triangle ABC\cong Rt\triangle AEC(HL)$,$\therefore AB=AE$,$\therefore AD=AB+12$.在$Rt\triangle ABD$中,$AB^2+BD^2=AD^2$,$\therefore AB^2+24^2=(AB+12)^2$,解得$AB=18$
11. 市政府准备对某公园进行小范围绿化.如图,现计划在公园一块四边形空地上种植草皮,测得∠B= 90°,AB= 24 m,BC= 7 m,CD= 15 m,AD= 20 m,求该四边形空地的面积.

答案:连接AC.$\because \angle B=90^\circ$,$AB=24\ m$,$BC=7\ m$,$\therefore AC=\sqrt{AB^2+BC^2}=\sqrt{24^2+7^2}=25(m)$. $\because CD=15\ m$,$AD=20\ m$,$\therefore 15^2+20^2=25^2$,即$DC^2+AD^2=AC^2$,$\therefore \triangle ACD$是直角三角形.$\therefore S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=\frac{1}{2}\cdot AB\cdot BC+\frac{1}{2}\cdot AD\cdot DC=\frac{1}{2}×24×7+\frac{1}{2}×20×15=234(m^2)$