1. 填空:
(1)一个直角三角形的三边从小到大依次为x,16,20,则x=
12
.
(2)在△ABC中,∠C= 90°,AB= 10,AC= 6,则另一边BC=
8
,面积为
24
,边AB上的高为
4.8
.
(3)若一个长方形的长与宽分别为5和12,则它的对角线的长为
13
.
答案:(1)12 (2)8,24,4.8 (3)13
解析:
(1)12
(2)8,24,4.8
(3)13
2. 观察下面几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25.请你写出满足以上规律的第④组勾股数:
9,40,41
.
答案:9,40,41
3. 如图,一艘船位于灯塔P的南偏东60°方向,距离灯塔12 n mile的A处,它沿正北方向航行到达位于灯塔正东方向的B处,此时船与灯塔P的距离为
$\sqrt{108}$
n mile.(1 n mile= 1 852 m)
答案:$\sqrt{108}$
4. 如图,在Rt△ABC中,∠ACB= 90°,若AB= 17,则正方形AEDC和正方形BCGF的面积之和为(
B
)
A.225
B.289
C.324
D.170
答案:B
解析:
在Rt△ABC中,∠ACB=90°,AB=17。
由勾股定理得:AC²+BC²=AB²=17²=289。
因为正方形AEDC的面积为AC²,正方形BCGF的面积为BC²,
所以两正方形面积之和为AC²+BC²=289。
答案:B
5. 如图,将一支铅笔放在圆柱形笔筒中,笔筒的内部底面直径是9 cm,内壁高12 cm.若这支铅笔长18 cm,则这支铅笔在笔筒外面部分的长度不可能是(
A
)
A.2 cm
B.3 cm
C.4 cm
D.6 cm
答案:A
解析:
当铅笔斜放时,在笔筒内部的长度最长,此时铅笔、笔筒底面直径和内壁高构成直角三角形。底面直径为$9\,cm$,内壁高为$12\,cm$,根据勾股定理,内部最长长度为$\sqrt{9^{2}+12^{2}}=\sqrt{81 + 144}=\sqrt{225}=15\,cm$。铅笔长$18\,cm$,则外部最短长度为$18 - 15=3\,cm$。所以外部长度不可能小于$3\,cm$,答案是A。
6. 已知一个直角三角形的两边长分别为3和5,则第三边长为(
C
)
A.4
B.2或√34
C.4或√34
D.2或√24
答案:C
解析:
情况1:若3和5为直角边,第三边长为$\sqrt{3^{2}+5^{2}}=\sqrt{34}$;
情况2:若5为斜边,3为直角边,第三边长为$\sqrt{5^{2}-3^{2}}=4$;
综上,第三边长为4或$\sqrt{34}$,答案选C。
7. 如图,在长方形纸片ABCD中,AB= 3 cm,AD= 9 cm,将此长方形纸片折叠,使点B与点D重合,折痕为EF,则△ABE的面积为(
C
)
A.3 cm² B.4 cm² C.6 cm² D.12 cm²
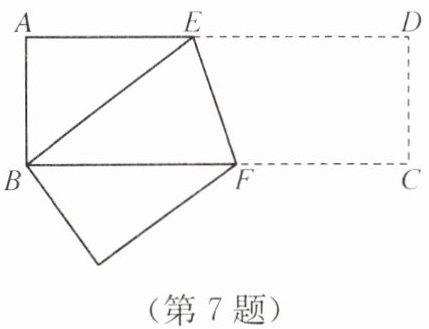
答案:C
解析:
设 $ AE = x \, cm $,则 $ DE = AD - AE = 9 - x \, cm $。
由折叠性质得 $ BE = DE = 9 - x \, cm $。
在 $ Rt\triangle ABE $ 中,$ AB^2 + AE^2 = BE^2 $,即 $ 3^2 + x^2 = (9 - x)^2 $。
展开得 $ 9 + x^2 = 81 - 18x + x^2 $,化简得 $ 18x = 72 $,解得 $ x = 4 $。
$ S_{\triangle ABE} = \frac{1}{2} × AB × AE = \frac{1}{2} × 3 × 4 = 6 \, cm^2 $。
答案:C
8. 如图,“赵爽弦图”由四个全等的直角三角形围成,在Rt△ABC中,AC= b,BC= a,∠ACB= 90°,若图中大正方形的面积为36,小正方形的面积为9,则$(a+b)^2$的值为______.

63
答案:63
解析:
大正方形面积为 $36$,则其边长为 $\sqrt{36}=6$,即直角三角形斜边 $AB=6$,由勾股定理得 $a^2 + b^2 = 6^2 = 36$。
小正方形面积为 $9$,则其边长为 $\sqrt{9}=3$,即 $b - a = 3$(假设 $b > a$)。
$(a + b)^2 = a^2 + 2ab + b^2 = (a^2 + b^2) + 2ab$,又 $(b - a)^2 = b^2 - 2ab + a^2 = 9$,即 $36 - 2ab = 9$,解得 $2ab = 27$,故 $(a + b)^2 = 36 + 27 = 63$。
63