2025年同步练习江苏八年级数学上册苏科版第65页解析答案

8. 若正方形 ABCD 的面积为 16,正方形内一点 P 到 CD 的距离与到点 A,B 的距离都是 d,则 d=

$\frac{5}{2}$

答案：$\frac{5}{2}$

解析：

以点$A$为原点，$AB$所在直线为$x$轴，$AD$所在直线为$y$轴建立平面直角坐标系。
因为正方形$ABCD$的面积为$16$，所以边长为$4$，则$A(0,0)$，$B(4,0)$，$CD$边所在直线为$y=4$。
设点$P(x,y)$，点$P$到$CD$的距离为$d$，则$4 - y = d$，即$y = 4 - d$。
点$P$到$A$，$B$的距离都是$d$，所以$\sqrt{x^2 + y^2} = d$，$\sqrt{(x - 4)^2 + y^2} = d$。
联立得$\sqrt{x^2 + y^2} = \sqrt{(x - 4)^2 + y^2}$，两边平方化简得$x = 2$。
将$x = 2$，$y = 4 - d$代入$\sqrt{x^2 + y^2} = d$，得$\sqrt{2^2 + (4 - d)^2} = d$，两边平方：$4 + (4 - d)^2 = d^2$，展开得$4 + 16 - 8d + d^2 = d^2$，解得$d = \frac{5}{2}$。
$\frac{5}{2}$

9. 如图,在△ABC 和△DBC 中,∠A= ∠D= 90°,BD 平分∠ABC,若 BC= 5,CD= $\sqrt{5}$,则 AC 的长为

答案：4

10. 如图,在△ABC 中,AB= 11,BC= 7,AC= 12. 求△ABC 的面积.

答案：
如图,过点 B 作 BD⊥AC,垂足为 D,则∠BDA=∠BDC=90°.设 AD=x,则 CD=12 - x.在 Rt△ABD 和 Rt△CBD 中,由勾股定理,得$BD^{2}=AB^{2}-AD^{2}=BC^{2}-CD^{2}$,即$11^{2}-x^{2}=7^{2}-(12 - x)^{2}$,解得 x = 9,
∴ AD = 9,
∴ BD = $\sqrt{AB^{2}-AD^{2}}=\sqrt{11^{2}-9^{2}}=\sqrt{40}$,
∴$S_{\triangle ABC}=\frac{1}{2}AC\cdot BD=\frac{1}{2}×12×\sqrt{40}=6\sqrt{40}$,即△ABC 的面积为$6\sqrt{40}$

11. 如图,在△ABC 中,AB= AC.
(1)若 P 是边 BC 的中点,连接 AP,求证：$BP\cdot CP= AB^{2}-AP^{2}$.
(2)若 P 是边 BC 上任意一点,上面的结论还成立吗？若成立,请证明；若不成立,请说明理由.

答案：

(1)
∵ AB = AC,P 是边 BC 上的中点,
∴ AP⊥BC,BP = PC.
∵$AB^{2}=AP^{2}+BP^{2}$,
∴$AB^{2}-AP^{2}=BP^{2}=BP\cdot CP$
(2) 成立.如图,过点 A 作 AM⊥BC,垂足为 M,
∵ AB = AC,
∴ BM = CM.
∵$AB^{2}=AM^{2}+BM^{2}$,$AP^{2}=AM^{2}+MP^{2}$,
∴$AB^{2}-AP^{2}=BM^{2}-MP^{2}=(BM + MP)\cdot (BM - MP)$.
∵ BM = CM,
∴ BM + MP = CM + PM = CP,
∴$AB^{2}-AP^{2}=BP\cdot CP$

12.【提出问题】已知 0＜x＜1,求$\sqrt{1+x^{2}}+\sqrt{1+(1-x)^{2}}$的最小值.
【分析问题】由勾股定理,可以通过构造直角三角形的方法,分别表示长度为$\sqrt{1+x^{2}}和\sqrt{1+(1-x)^{2}}$的线段,将代数求和问题转化为线段求和问题.
【解决问题】
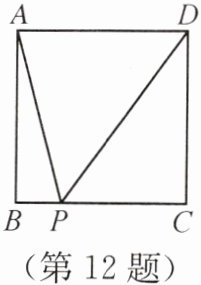
(1)如图,我们可以构造边长为 1 的正方形 ABCD,P 为边 BC 上的动点,设 BP= x,则 PC= 1-x.
① $AP^{2}$= ______,$PD^{2}$= ______；
② $\sqrt{1+x^{2}}+\sqrt{1+(1-x)^{2}}$可以表示为线段______与______之和.
(2)在(1)的条件下,已知 0＜x＜1,求$\sqrt{1+x^{2}}+\sqrt{1+(1-x)^{2}}$的最小值.

答案：

(1) ①$1 + x^{2}$,$1+(1 - x)^{2}$;② AP,DP
(2) 作点 A 关于直线 BC 的对称点 A',连接 PA',连接 DA'交 BC 于点 P',如图.由点 A,A'关于直线 BC 对称可得,AP = A'P,
∴ AP + DP = A'P + DP.根据两点之间线段最短可知,当点 P 与点 P'重合时,AP + DP = A'D,此时 AP + DP 最小.
∵ A'B = AB = 1,
∴ AA' = 2,
∴$A'D=\sqrt{AA'^{2}+AD^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$.
∴ 当 0 ＜ x ＜ 1 时,$\sqrt{1 + x^{2}}+\sqrt{1+(1 - x)^{2}}$的最小值为$\sqrt{5}$