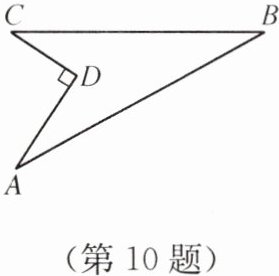
10. 如图,某住宅小区在施工过程中留下了一块空地,已知$AD= 4m$,$CD= 3m$,$\angle ADC= 90^\circ$,$AB= 13m$,$BC= 12m$,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米30元,用该草坪铺满这块空地共需花费多少元?
答案:连接 AC,在$Rt\triangle ACD$中,$\because AC^{2}=CD^{2}+AD^{2}=3^{2}+4^{2}=25$,$\therefore AC=5$.$\because AC^{2}+BC^{2}=5^{2}+12^{2}=169$,$AB^{2}=13^{2}=169$,$\therefore AC^{2}+BC^{2}=AB^{2}$,$\therefore \angle ACB=90^{\circ}$,该区域面积$=S_{\triangle ACB}-S_{\triangle ACD}=30-6=24(m^{2})$,铺满这块空地共需花费$=24×30=720$(元)
11. 清代扬州数学家罗士琳痴迷于研究勾股定理,提出推算勾股数的“罗士琳法则”,其中有一个法则是“如果k是大于2的偶数,那么k和k的一半的平方减1,k的一半的平方加1是一组勾股数”.
(1)按照这个法则,写出一组勾股数:______
3,4,5
(最大数不超过18).
(2)用含有k的等式表示“罗士琳法则”并证明.
当 k 大于 2 时,$k^{2}+\left \lbrack \left( \frac{1}{2}k\right)^{2}-1\right\rbrack^{2}=\left \lbrack \left( \frac{1}{2}k\right)^{2}+1\right\rbrack^{2}$. 证明:$\because$左边$=k^{2}+\left \lbrack \left( \frac{1}{2}k\right)^{2}-1\right\rbrack^{2}=k^{2}+\left \lbrack \frac{1}{4}k^{2}-1\right\rbrack^{2}=k^{2}+\frac{1}{16}k^{4}+1-\frac{1}{2}k^{2}=\frac{1}{16}k^{4}+\frac{1}{2}k^{2}+1$;右边$=\left \lbrack \left( \frac{1}{2}k\right)^{2}+1\right\rbrack^{2}=\left \lbrack \frac{1}{4}k^{2}+1\right\rbrack^{2}=\frac{1}{16}k^{4}+\frac{1}{2}k^{2}+1$.$\therefore$左边=右边,$\therefore$等式成立
答案:(1)3,4,5 (2)当 k 大于 2 时,$k^{2}+\left \lbrack \left( \frac{1}{2}k\right)^{2}-1\right\rbrack^{2}=\left \lbrack \left( \frac{1}{2}k\right)^{2}+1\right\rbrack^{2}$. 证明:$\because$左边$=k^{2}+\left \lbrack \left( \frac{1}{2}k\right)^{2}-1\right\rbrack^{2}=k^{2}+\left \lbrack \frac{1}{4}k^{2}-1\right\rbrack^{2}=k^{2}+\frac{1}{16}k^{4}+1-\frac{1}{2}k^{2}=\frac{1}{16}k^{4}+\frac{1}{2}k^{2}+1$;右边$=\left \lbrack \left( \frac{1}{2}k\right)^{2}+1\right\rbrack^{2}=\left \lbrack \frac{1}{4}k^{2}+1\right\rbrack^{2}=\frac{1}{16}k^{4}+\frac{1}{2}k^{2}+1$.$\therefore$左边=右边,$\therefore$等式成立
解析:
(1)6,8,10
(2)当$k$是大于2的偶数时,$k^{2}+\left[\left(\frac{1}{2}k\right)^{2}-1\right]^{2}=\left[\left(\frac{1}{2}k\right)^{2}+1\right]^{2}$
证明:左边$=k^{2}+\left[\left(\frac{1}{2}k\right)^{2}-1\right]^{2}=k^{2}+\left(\frac{1}{4}k^{2}-1\right)^{2}=k^{2}+\frac{1}{16}k^{4}-\frac{1}{2}k^{2}+1=\frac{1}{16}k^{4}+\frac{1}{2}k^{2}+1$
右边$=\left[\left(\frac{1}{2}k\right)^{2}+1\right]^{2}=\left(\frac{1}{4}k^{2}+1\right)^{2}=\frac{1}{16}k^{4}+\frac{1}{2}k^{2}+1$
$\because$左边=右边
$\therefore$等式成立
12. 如图,P是等边三角形ABC内一点,且$PA= 6$,$PB= 8$,$PC= 10$,若将$\triangle PAC$绕点A按逆时针方向旋转后得到$\triangle P'AB$,求$PP'的长和\angle APB$的大小.

答案:$\because \triangle ABC$是等边三角形,$\therefore \angle CAB=60^{\circ}$.$\because \triangle PAC$绕点 A 按逆时针方向旋转后得到$\triangle P'AB$,$\therefore \angle PAP'=\angle CAB=60^{\circ}$,$AP=AP'$,$P'B=PC=10$,$\therefore \triangle APP'$是等边三角形.$\therefore PP'=AP=6$,$\angle APP'=60^{\circ}$.$\because PB^{2}+PP'^{2}=8^{2}+6^{2}=100=P'B^{2}$,$\therefore \triangle BPP'$是直角三角形.$\therefore \angle P'PB=90^{\circ}$,$\therefore \angle APB=\angle APP'+\angle P'PB=150^{\circ}$