8. 如图,AD,CE 都是△ABC 的中线,连接ED,△ABC 的面积是12,则△BDE 的面积是(
A
)
A.3
B.4
C.5
D.6
答案:A
解析:
∵AD是△ABC的中线,
∴BD = $\frac{1}{2}$BC,$S_{\triangle ABD} = \frac{1}{2}S_{\triangle ABC}$。
∵$S_{\triangle ABC} = 12$,
∴$S_{\triangle ABD} = \frac{1}{2}×12 = 6$。
∵CE是△ABC的中线,
∴E是AB的中点,
∴BE = $\frac{1}{2}$AB,$S_{\triangle BDE} = \frac{1}{2}S_{\triangle ABD}$。
∴$S_{\triangle BDE} = \frac{1}{2}×6 = 3$。
A
9. 如图,在△ABC 中,AB= 2024,AC= 2018,AD 为中线,则△ABD 与△ACD 的周长之差为
6
.
答案:6
解析:
∵AD为中线,
∴BD=CD。
△ABD的周长=AB+BD+AD,
△ACD的周长=AC+CD+AD,
周长之差=(AB+BD+AD)-(AC+CD+AD)=AB-AC。
∵AB=2024,AC=2018,
∴AB-AC=2024-2018=6。
6
10. 请用不同的方法,将△ABC 分割成面积相等的四部分.
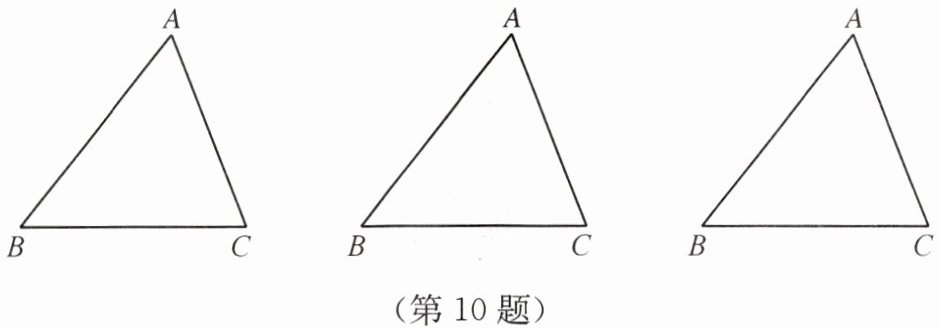
答案:如图,答案不唯一


11. 如图,在△ABC 中,BE,CD 都是△ABC 的角平分线,CD 与BE 交于点O,∠A= 70°,求∠BOC 的大小.

答案:
∵ BE,CD 是△ABC 的角平分线,
∴ ∠OBC = $\frac{1}{2}$∠ABC,
∠OCB=$\frac{1}{2}$∠ACB,
∴ ∠OBC + ∠OCB = $\frac{1}{2}$(∠ABC + ∠ACB).
∵ ∠ABC + ∠ACB = 180° - ∠A,
∴ ∠BOC = 180° - (∠OBC +
∠OCB)=180° - $\frac{1}{2}$(180° - ∠A)=125°
12. 如图,在△ABC 中,∠C= 90°,AC= 8cm,BC= 6cm,AB= 10cm,若动点P 从点C 开始,按C→A→B→C 的路径运动,且速度为3cm/s,设运动的时间为t s.

(1)当t= ______s时,CP 把△ABC 的周长分成相等的两部分.
(2)当t= ______s时,CP 把△ABC 的面积分成相等的两部分.
(3)当t为何值时,△BCP 的面积为$18cm^2?$
答案:(1) 4
(2) $\frac{13}{3}$
(3) 如图①,当点 P 在边 AC 上时,
∵ $S_{\triangle BCP}$ = $\frac{1}{2}$×6×3t=18,
∴ t=2. 如图②,当点 P 在边 AB 上时,过点 C 作 CD⊥AB,垂足为 D.
∵ $S_{\triangle ABC}$ = $\frac{1}{2}$×AC×BC = $\frac{1}{2}$×AB×CD,
∴ CD = $\frac{6×8}{10}$ = $\frac{24}{5}$.
∵ $S_{\triangle BCP}$ = $\frac{1}{2}$×(18 - 3t)×$\frac{24}{5}$=18,
∴ t = $\frac{7}{2}$. 综上所述:当 t=2 或$\frac{7}{2}$时,$\triangle BCP$ 的面积为 18 $cm^2$
