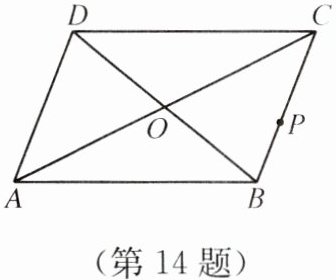
14. 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA= OC,OB= OD.
(1)求证:AD= BC;
(2)已知P为边BC上的一点,请只用直尺(不带刻度)作图:在边AD上作一点Q,使得AQ= CP. 保留作图痕迹,并证明AQ= CP.
答案:
(1) 因为 OA=OC,OB=OD,∠AOD=∠COB,所以△AOD≌△COB,则 AD=BC
(2) 作图方法:连接 PO 并延长 PO 交 AD 于点 Q. 由
(1)得△AOD≌△COB,则∠DAO=∠BCO,又 OA=OC,∠AOQ=∠COP,所以△AOQ≌△COP,故 AQ=CP
15. 如图,在四边形ABCD中,AB= AD,∠A= ∠C= 90°,且BC+CD= 6. 求四边形ABCD的面积.

答案:连接 CA,将线段 CA 绕点 A 按顺时针方向旋转 90°,得到线段 EA,连接 BE. 因为∠DAB=∠CAE=90°,所以∠DAC=∠BAE. 又因为 AB=AD,AC=AE,故△DAC≌△BAE,故∠D=∠ABE,DC=BE. 因为∠A=∠C=90°,所以∠B+∠D=180°,故∠ABC+∠D=180°,即∠ABC+∠ABE=180°,故 B,C,E 三点共线. 所以 CE=BC+BE=BC+CD=6,而△ACE 是等腰直角三角形,其斜边 CE 上的高为斜边的一半,即 6,所以 $S_{四边形ABCD}=S_{\triangle ACE}=\frac{1}{2}×6×3=9$
解析:
连接 $ CA $,将线段 $ CA $ 绕点 $ A $ 按顺时针方向旋转 $ 90^\circ $,得到线段 $ EA $,连接 $ BE $。
因为 $ \angle DAB = \angle CAE = 90^\circ $,所以 $ \angle DAC = \angle BAE $。
又因为 $ AB = AD $,$ AC = AE $,故 $ \triangle DAC \cong \triangle BAE $,因此 $ \angle D = \angle ABE $,$ DC = BE $。
由于 $ \angle A = \angle C = 90^\circ $,四边形内角和为 $ 360^\circ $,则 $ \angle ABC + \angle D = 180^\circ $,即 $ \angle ABC + \angle ABE = 180^\circ $,所以 $ B $,$ C $,$ E $ 三点共线。
因此 $ CE = BC + BE = BC + CD = 6 $。
$ \triangle ACE $ 是等腰直角三角形,其斜边上的高为斜边的一半,即 $ \frac{6}{2} = 3 $。
所以 $ S_{四边形ABCD} = S_{\triangle ACE} = \frac{1}{2} × 6 × 3 = 9 $。
答案:$ 9 $