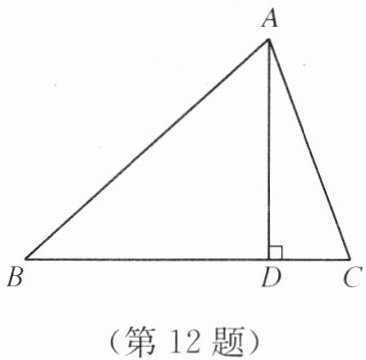
12. 如图,在△ABC中,已知AB>AC,AD⊥BC. 求证:BD>DC.
答案:因为 AB>AC,所以∠B<∠C. 因为∠B+∠BAD=∠C+∠CAD=90°,所以∠BAD>∠CAD,所以可作∠DAE=∠CAD,其中点 E 落在线段 BD 上. 根据 AD 是△AEC 的角平分线、高,可知 AD 也是中线,所以 ED=DC. 而 BD=BE+ED,所以 BD>DC
解析:
证明:在△ABC中,AB>AC,所以∠B<∠C。
因为AD⊥BC,所以∠ADB=∠ADC=90°,
则∠B+∠BAD=90°,∠C+∠CAD=90°,
又∠B<∠C,故∠BAD>∠CAD。
在BD上取点E,使∠DAE=∠CAD,
因为AD是△AEC的角平分线且AD⊥EC,
所以AD是△AEC的中线,即ED=DC。
又BD=BE+ED,且BE>0,
所以BD>ED=DC,即BD>DC。
13. 如图,在△ABC中,D为边BC的中点,DE⊥BC,垂足为D,交∠BAC的平分线于点E,EF⊥AB,垂足为F,EG⊥AC,交AC的延长线于点G,线段BF与线段CG的长有怎样的大小关系?证明你的结论.

答案:连接 EB,EC,因为 AE 是∠BAC 的平分线,且 EF⊥AB,垂足为 F,EG⊥AC,垂足为 G,所以 EF=EG. 又因为 ED⊥BC,垂足为 D,D 是 BC 的中点,所以 EB=EC. 所以 Rt△EFB≌Rt△EGC(HL),故 BF=CG
解析:
BF=CG
证明:连接EB,EC。
∵AE是∠BAC的平分线,EF⊥AB,EG⊥AC,
∴EF=EG。
∵D为BC的中点,DE⊥BC,
∴EB=EC。
在Rt△EFB和Rt△EGC中,
$\begin{cases}EB=EC \\EF=EG\end{cases}$
∴Rt△EFB≌Rt△EGC(HL),
∴BF=CG。