2. 在$Rt\triangle ABC$中,$\angle ACB= 90^\circ$,D是AB的中点,CD= 5,则AB=
10
.
答案:10
解析:
在$Rt\triangle ABC$中,$\angle ACB=90^\circ$,D是AB的中点。根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,可得$CD=\frac{1}{2}AB$。已知$CD=5$,则$AB=2CD=2×5=10$。
10
3. 直角三角形斜边上的高与中线分别是5和6,则它的面积是
30
.
答案:30
解析:
在直角三角形中,斜边上的中线等于斜边的一半。已知斜边上的中线是6,所以斜边的长为$2×6 = 12$。
直角三角形的面积可以表示为$\frac{1}{2}× 斜边× 斜边上的高$,已知斜边上的高是5,所以该直角三角形的面积为$\frac{1}{2}×12×5 = 30$。
30
4. 如图,在$\triangle ABC$中,AB= AC= 10,BC= 8,AD平分$\angle BAC$,交BC于点D,DE是$\triangle ADC$的中线,连接DE,则$\triangle CDE$的周长为
14
.
答案:14
解析:
在$\triangle ABC$中,$AB=AC=10$,$AD$平分$\angle BAC$,根据等腰三角形三线合一性质,$AD$垂直平分$BC$。
因为$BC=8$,所以$CD=\frac{1}{2}BC = 4$。
在$Rt\triangle ADC$中,$AC=10$,$CD=4$,由勾股定理得$AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{10^{2}-4^{2}}=\sqrt{100 - 16}=\sqrt{84}=2\sqrt{21}$。
$DE$是$\triangle ADC$的中线,所以$E$为$AC$中点,$CE=\frac{1}{2}AC = 5$,$DE=\frac{1}{2}AC = 5$(直角三角形斜边中线等于斜边一半)。
$\triangle CDE$的周长为$CD + CE + DE=4 + 5 + 5=14$。
14
5. 如图,在$\triangle ABC$中,$\angle ACB= 90^\circ$,$\angle ABC= 60^\circ$,BD平分$\angle ABC$,P是BD的中点,若AD= 6,则CP的长为______
3
.
答案:3
解析:
在$\triangle ABC$中,$\angle ACB=90^\circ$,$\angle ABC=60^\circ$,则$\angle BAC=30^\circ$。设$BC=x$,则$AB=2x$,$AC=\sqrt{AB^2 - BC^2}=\sqrt{(2x)^2 - x^2}=\sqrt{3}x$。
因为BD平分$\angle ABC$,所以$\angle ABD = \angle CBD = 30^\circ$。在$\triangle BCD$中,$\angle CBD = 30^\circ$,$\angle BCD = 90^\circ$,所以$CD = BC \tan 30^\circ = x \cdot \frac{\sqrt{3}}{3} = \frac{\sqrt{3}}{3}x$。
则$AD = AC - CD = \sqrt{3}x - \frac{\sqrt{3}}{3}x = \frac{2\sqrt{3}}{3}x$。已知$AD = 6$,所以$\frac{2\sqrt{3}}{3}x = 6$,解得$x = 3\sqrt{3}$。
在$\triangle BCD$中,$BC = 3\sqrt{3}$,$CD = \frac{\sqrt{3}}{3} × 3\sqrt{3} = 3$,所以$BD = \sqrt{BC^2 + CD^2} = \sqrt{(3\sqrt{3})^2 + 3^2} = \sqrt{27 + 9} = \sqrt{36} = 6$。
因为P是BD的中点,所以$CP = \frac{1}{2}BD = \frac{1}{2} × 6 = 3$。
3
6. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^\circ$,D为AB的中点,$\angle A= 30^\circ$,BC= 2. 求CD的长.
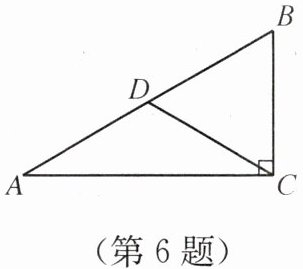
答案:因为∠ACB=90°,∠A=30°,所以 BC= $\frac{1}{2}$AB,又 BC=2,则 AB=4.又 D 为 AB 的中点,则 CD= $\frac{1}{2}$AB=2
解析:
在$Rt\triangle ABC$中,$\angle ACB=90^\circ$,$\angle A=30^\circ$,所以$BC=\frac{1}{2}AB$。
因为$BC=2$,所以$AB=2BC=4$。
又因为$D$为$AB$的中点,所以$CD=\frac{1}{2}AB=\frac{1}{2}×4=2$。
故$CD$的长为$2$。
7. 若一个三角形一边的中线等于这条边的一半,则这个三角形为
直角
三角形.
答案:直角
8. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^\circ$,D为边AB的中点,$\angle B= 30^\circ$,点E在BC上,且CE= AC,则$\angle CDE$的大小为
75
°.
答案:75
解析:
设$AC = x$,在$Rt\triangle ABC$中,$\angle ACB = 90^\circ$,$\angle B = 30^\circ$,则$AB = 2AC = 2x$,$BC=\sqrt{AB^2 - AC^2}=\sqrt{(2x)^2 - x^2}=\sqrt{3}x$。
因为$D$为$AB$中点,所以$CD = AD = BD = x$,$\angle ACD=\angle A = 60^\circ$。
又因为$CE = AC = x$,所以$\triangle CDE$中,$CD = CE = x$,$\angle DCE=\angle ACB-\angle ACD = 90^\circ - 60^\circ=30^\circ$。
故$\angle CDE=\frac{180^\circ-\angle DCE}{2}=\frac{180^\circ - 30^\circ}{2}=75^\circ$。
75
9. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^\circ$,$\angle A= 65^\circ$,$CD\perp AB$,垂足为D,E是边BC的中点,连接ED,则$\angle DEC$的大小为(
D
)
A.25°
B.30°
C.40°
D.50°
答案:D
解析:
在$Rt\triangle ABC$中,$\angle ACB=90^\circ$,$\angle A=65^\circ$,则$\angle B=90^\circ - 65^\circ=25^\circ$。
因为$CD\perp AB$,所以$\angle CDB=90^\circ$,$\triangle CDB$是直角三角形。
由于E是边BC的中点,直角三角形斜边上的中线等于斜边的一半,故$DE=BE=CE$。
所以$\angle EDB=\angle B=25^\circ$,则$\angle DEC=\angle EDB+\angle B=25^\circ + 25^\circ=50^\circ$。
D