10. 如图,在等边三角形纸片ABC中,点E在边AC上,点F在边AB上,沿EF折叠使点A落在边BC上的点D处,若∠BFD= 80°,则∠DEF=
70
°.
答案:70
11. 已知a,b,c是△ABC的三边,且$a^2+b^2+c^2= ab+ac+bc$,则△ABC是(
C
)
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
答案:C
解析:
已知$a^2 + b^2 + c^2 = ab + ac + bc$,等式两边同时乘以2得:$2a^2 + 2b^2 + 2c^2 = 2ab + 2ac + 2bc$,移项整理得:$(a^2 - 2ab + b^2) + (a^2 - 2ac + c^2) + (b^2 - 2bc + c^2) = 0$,即$(a - b)^2 + (a - c)^2 + (b - c)^2 = 0$。因为平方数具有非负性,所以$a - b = 0$,$a - c = 0$,$b - c = 0$,解得$a = b = c$,故$\triangle ABC$是等边三角形。
C
12. 如图,在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,点B,P,Q在同一条直线上,∠ABP= ∠ACQ,BP= CQ,△APQ是什么形状的三角形?证明你的结论.
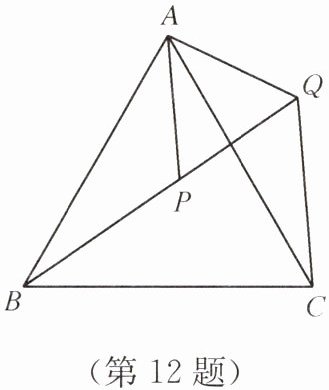
答案:△APQ为等边三角形.因为△ABC为等边三角形,所以AB=AC.所以△ABP≌△ACQ(SAS),则AP=AQ,∠BAP=∠CAQ.因为∠BAC=∠BAP+∠PAC=60°,所以∠PAQ=∠CAQ+∠PAC=60°,所以△APQ是等边三角形
解析:
△APQ是等边三角形.
证明:
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
在△ABP和△ACQ中,
$\left\{\begin{array}{l}AB=AC\\ \angle ABP=\angle ACQ\\ BP=CQ\end{array}\right.$,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=∠BAP+∠PAC=60°.
∵AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形.
13. 在等边三角形ABC中,E是边AB上的动点,点E与点A,B不重合,点D在CB的延长线上,且EC= ED.
(1)如图①,若E是AB的中点,求证:BD= AE.
(2)如图②,若E不是AB的中点,则(1)中的结论“BD= AE”能否成立?若不成立,请直接写出BD与AE的数量关系;若成立,请加以证明.

答案:
(1) 因为△ABC是等边三角形,所以∠ABC=∠ACB=60°,因为点E是AB的中点,所以CE平分∠ACB,AE=BE,所以∠BCE=30°,因为ED=EC,所以∠D=∠BCE=30°.因为∠ABC=∠D+∠BED,所以∠BED=30°,所以∠D=∠BED,则BD=BE.故AE=DB
(2) AE=DB.理由:过点E作EF//BC交AC于点F.所以∠AEF=∠ABC,∠AFE=∠ACB.因为△ABC是等边三角形,所以∠ABC=∠ACB=∠A=60°,AB=AC=BC,所以∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°,所以△AEF是等边三角形.所以∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°.因为DE=EC,所以∠D=∠ECD,所以∠BED=∠ECF.所以△DEB≌△ECF(AAS),所以DB=EF,所以AE=BD