8. 已知a,b,c是一个三角形的三边长,回答下列问题.
(1)比较大小:a-b-c
<
0,b-a-c
<
0,c+b-a
>
0.(填“>”“<”或“=”)
(2)化简:|a-b-c|+|b-a-c|-|c+b-a|.
原式=b+c-a+a+c-b-c-b+a=a-b+c
答案:
(1) <,<,>
(2) 原式=b+c-a+a+c-b-c-b+a=a-b+c
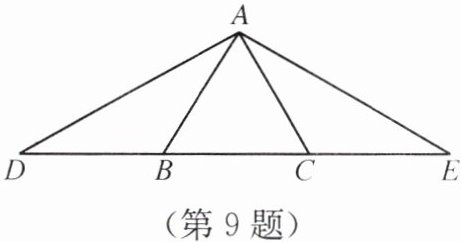
9. 如图,AB>AC,∠BDA= ∠BAD,∠CEA= ∠EAC.求证:AD>AE.
答案:
∵AB>AC,
∴∠ACB>∠ABC.
∵∠ACB=∠CAE+∠AEC=2∠AEC,∠ABC=∠BAD+∠ADB=2∠ADB,
∴∠AEC>∠ADB,
∴AD>AE
10. 观察并探究下列问题:
(1)如图①,在△ABC中,P为边BC上的一点,则BP+PC______AB+AC(填“>”“<”或“=”).
(2)将图①中点P移到△ABC内,得图②,比较△BPC的周长与△ABC的周长的大小,并说明理由.
(3)将图②中点P变为两个点$P_1,P_2,$得图③,比较四边形$BP_1P_2C$的周长与△ABC的周长的大小,并说明理由.

答案:(1) <
(2) △BPC的周长比较小.理由:如图①,延长BP交AC于点M,在△ABM中,BP+PM<AB+AM,在△PMC中,PC<PM+MC,两式相加得BP+PC<AB+AC,所以△BPC的周长比△ABC的周长小
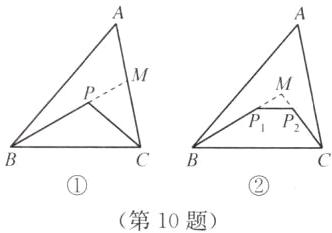
(3) 四边形BP₁P₂C的周长<△ABC的周长,理由:如图②,分别延长BP₁,CP₂交于点M,由
(2)知,BM+CM<AB+AC,因为P₁P₂<P₁M+P₂M,可得BP₁+P₁P₂+P₂C<BM+CM<AB+AC,得证