1. 三角形的任意两边之和
大于
第三边,任意两边之差
小于
第三边(填“大于”或“小于”).
答案:大于,小于
2. 在同一个三角形中,较大的边所对的角也
比较大
,较大的角所对的边也
比较大
.(简称“
大边对大角,大角对大边
”)
答案:比较大,比较大,大边对大角,大角对大边
3. 若一个三角形的两边长分别为3,5,则它的第三边的长可能是(
C
)
A.1
B.2
C.6
D.8
答案:C
解析:
设第三边的长为$x$。
根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,得:
$5 - 3 < x < 5 + 3$,即$2 < x < 8$。
选项中符合条件的是$6$。
C
4. 若△ABC中最长的边所对的角是锐角,则△ABC(
A
)
A.一定是锐角三角形
B.一定是钝角三角形
C.可能是直角三角形
D.形状无法判断
答案:A
解析:
在△ABC中,最长边所对的角最大。
因为最长边所对的角是锐角,所以三角形的三个角均为锐角。
因此,△ABC一定是锐角三角形。
A
5. 在△ABC中,AD⊥BC.当AB>AC时,比较∠BAD与∠CAD的大小,并说明理由.
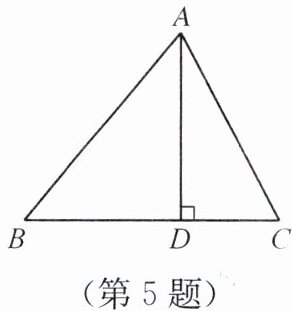
答案:
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∴∠BAD=90°-∠B,∠CAD=90°-∠C.
∵AB>AC,
∴∠C>∠B,
∴∠BAD>∠CAD
6. 在△ABC中,有两条边的长是2和5,且△ABC的第三边长是偶数,则此三角形的周长为(
D
)
A.11
B.12
C.13
D.11或13
答案:D
解析:
设第三边长为$x$。
根据三角形三边关系:两边之和大于第三边,两边之差小于第三边。
$5 - 2 < x < 5 + 2$,即$3 < x < 7$。
因为第三边长$x$是偶数,所以$x = 4$或$x = 6$。
当$x = 4$时,周长为$2 + 5 + 4 = 11$;
当$x = 6$时,周长为$2 + 5 + 6 = 13$。
此三角形的周长为11或13。
D
7. 已知三角形的三边长分别为4,x,11,化简:|x-5|+|x-16|=
11
.
答案:11
解析:
根据三角形三边关系,两边之和大于第三边,两边之差小于第三边。
可得:$11 - 4 < x < 11 + 4$,即$7 < x < 15$。
因为$7 < x < 15$,所以$x - 5 > 0$,$x - 16 < 0$。
则$|x - 5| = x - 5$,$|x - 16| = 16 - x$。
$|x - 5| + |x - 16| = (x - 5) + (16 - x) = 11$
11