9. 如图,在$\triangle ABC$中,$AC= BC$,$D为边AB$的中点,$E为BC$延长线上的一点,过点$E作EF\perp AB$,垂足为$F$,交$AC于点G$.
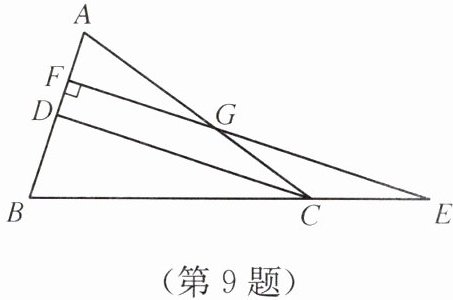
(1)求证:$EF// CD$;
(2)求证:$\triangle CEG$是等腰三角形.
答案:
(1) $\because AC=BC$,D为边AB的中点,$\therefore CD\perp AB$。$\because EF\perp AB$,$\therefore EF// CD$
(2) $\because AC=BC$,D为边AB的中点,$\therefore \angle ACD=\angle BCD$。$\because EF// CD$,$\therefore \angle ACD=\angle EGC$,$\angle BCD=\angle E$,$\therefore \angle EGC=\angle E$,$\therefore CG=CE$,$\therefore \triangle CEG$是等腰三角形
10. 在$\triangle ABC$中,$D是边BC$上的一点,$\angle BDA= \angle BAC$.

(1)如图①,求证:$\angle 1= \angle C$;
(2)如图②,$BE平分\angle ABC$,分别交$AC$,$AD于点E$,$F$. 求证:$AE= AF$.
答案:
(1) $\because \angle B+\angle 1+\angle BDA=180^\circ$,$\angle B+\angle C+\angle BAC=180^\circ$,$\therefore \angle 1=180^\circ-\angle B-\angle BDA$,$\angle C=180^\circ-\angle B-\angle BAC$。$\because \angle BDA=\angle BAC$,$\therefore 180^\circ-\angle B-\angle BDA=180^\circ-\angle B-\angle BAC$,$\therefore \angle 1=\angle C$
(2) $\because BE$平分$\angle ABC$,$\therefore \angle ABE=\angle CBE=\frac{1}{2}\angle ABC$。$\because \angle BFD=\angle 1+\angle ABE$,$\angle AEF=\angle C+\angle CBE$,$\therefore \angle BFD=\angle AEF$。$\because \angle BFD=\angle AFE$,$\therefore \angle AEF=\angle AFE$,$\therefore AE=AF$
11. 如图,在$\triangle ABC$中,$AO平分\angle BAC$,$\angle 1= \angle 2$. 求证:$\triangle ABC$是等腰三角形.

答案:过点O作$OD\perp AB$,垂足为D,过点O作$OE\perp AC$,垂足为E。$\because OD\perp AB$,$OE\perp AC$,AO平分$\angle BAC$,$\therefore OD=OE$。$\because \angle 1=\angle 2$,$\therefore OB=OC$。在$Rt\triangle BDO$和$Rt\triangle CEO$中,$\because Rt\triangle DOB\cong Rt\triangle EOC(HL)$,$\therefore \angle DBO=\angle ECO$,$\therefore \angle ABC=\angle ACB$,$\therefore AB=AC$
解析:
证明:过点$O$作$OD\perp AB$,垂足为$D$,过点$O$作$OE\perp AC$,垂足为$E$。
$\because OD\perp AB$,$OE\perp AC$,$AO$平分$\angle BAC$,
$\therefore OD=OE$。
$\because \angle 1=\angle 2$,
$\therefore OB=OC$。
在$Rt\triangle BDO$和$Rt\triangle CEO$中,
$\begin{cases} OB=OC \\ OD=OE \end{cases}$
$\therefore Rt\triangle BDO\cong Rt\triangle CEO(HL)$。
$\therefore \angle DBO=\angle ECO$。
$\because \angle 1=\angle 2$,
$\therefore \angle ABC=\angle ACB$。
$\therefore AB=AC$。
$\therefore \triangle ABC$是等腰三角形。