1. 有
两个角相等
的三角形是等腰三角形(简称“等角对等边”).
答案:两个角相等
2. 在$\triangle ABC$中,$\angle A= 100^\circ$,当$\angle B= $
40
$^\circ$时,$\triangle ABC$是等腰三角形.
答案:40
解析:
当$\angle A$为顶角时,$\angle B=\angle C=\frac{180^\circ - 100^\circ}{2}=40^\circ$;当$\angle A$为底角时,$\angle B=100^\circ$,此时$\angle A+\angle B=200^\circ>180^\circ$,不符合三角形内角和定理,舍去。故$\angle B=40^\circ$。
3. 在$\triangle ABC$中,$AD$是中线,点$D到边AB$,$AC$的距离相等,则$\triangle ABC$一定是 (
B
)
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
答案:B
解析:
∵AD是△ABC的中线,
∴BD=CD。
∵点D到边AB,AC的距离相等,
∴点D在∠BAC的平分线上,即AD平分∠BAC。
过点D作DE⊥AB于E,DF⊥AC于F,则DE=DF。
在Rt△BDE和Rt△CDF中,
∵BD=CD,DE=DF,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形。
B
4. 如图,已知$A$,$B$是格点,若$C$也是格点,且使得$\triangle ABC$为等腰三角形,则符合条件的点$C$有 (
A
)
A.8个
B.9个
C.10个
D.11个
答案:A
解析:
以A为顶点:AB中垂线与格点交点有4个;以B为顶点:AB中垂线与格点交点有4个;以C为顶点:AB为底边,无其他格点。共4+4=8个。A
5. 如图,在$\triangle ABC$中,$\angle A= 36^\circ$,$\angle B= 72^\circ$,$CD平分\angle ACB$,$DE// AC$,则图中共有等腰三角形 (
D
)
A.2个
B.3个
C.4个
D.5个
答案:D
解析:
在$\triangle ABC$中,$\angle A=36^\circ$,$\angle B=72^\circ$,则$\angle ACB=180^\circ - 36^\circ - 72^\circ=72^\circ$,$\angle ACB=\angle B$,故$\triangle ABC$是等腰三角形。
$CD$平分$\angle ACB$,则$\angle ACD=\angle BCD=\frac{1}{2}\angle ACB=36^\circ$。
在$\triangle ACD$中,$\angle A=36^\circ$,$\angle ACD=36^\circ$,$\angle A=\angle ACD$,故$\triangle ACD$是等腰三角形。
在$\triangle BCD$中,$\angle B=72^\circ$,$\angle BCD=36^\circ$,$\angle CDB=180^\circ - 72^\circ - 36^\circ=72^\circ$,$\angle B=\angle CDB$,故$\triangle BCD$是等腰三角形。
$DE// AC$,则$\angle CDE=\angle ACD=36^\circ$,$\angle ADE=\angle A=36^\circ$。
在$\triangle CDE$中,$\angle CDE=\angle DCE=36^\circ$,故$\triangle CDE$是等腰三角形。
在$\triangle BDE$中,$\angle ADE=36^\circ$,$\angle CDB=72^\circ$,$\angle EDB=180^\circ - \angle ADE - \angle CDB=72^\circ$,$\angle B=72^\circ$,$\angle EDB=\angle B$,故$\triangle BDE$是等腰三角形。
综上,图中共有5个等腰三角形,答案选D。
6. 如图,在四边形$ABCD$中,$AD// BC$,$DC= AB$,$BF平分\angle ABC$,交$AD于点F$,$CE平分\angle BCD$,交$AD于点E$,$AB= 6$,$EF= 2$,则$AD$的长为______
10
.
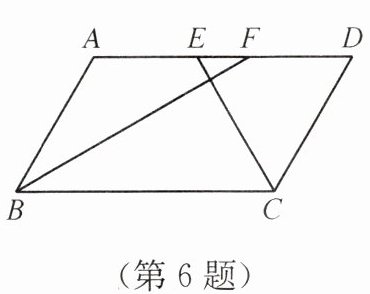
答案:10
解析:
∵AD//BC,DC=AB,
∴四边形ABCD是等腰梯形或平行四边形。
若为平行四边形,则AB=DC且AD//BC,此时∠ABC=∠BCD,BF、CE为角平分线,易证AE=DF,设AE=DF=x,AD=AE+EF+FD=2x+2,又AB=6,在平行四边形中AB=DC=6,由角平分线及平行性质得AF=AB=6,DE=DC=6,AF=AE+EF=x+2=6,x=4,AD=2×4+2=10;
若为等腰梯形,同理可得AF=AB=6,DE=DC=6,AD=AF+FD=6+(DE-EF)=6+(6-2)=10。
综上,AD=10。
7. 如图,$\triangle ABC的顶点A$,$C在直线l$上,$\angle B= 120^\circ$,$\angle ACB= 40^\circ$,若点$P在直线l$上运动,当$\triangle ABP$成为等腰三角形时,则$\angle ABP$大小是
$10^\circ$或$20^\circ$或$80^\circ$或$140^\circ$
.
答案:$10^\circ$或$20^\circ$或$80^\circ$或$140^\circ$
解析:
在$\triangle ABC$中,$\angle B=120^\circ$,$\angle ACB=40^\circ$,则$\angle BAC=180^\circ - 120^\circ - 40^\circ=20^\circ$。点$P$在直线$l$上,分以下情况讨论:
1. 当$AB=AP$时,
点$P$在$A$左侧:$\angle ABP=\angle APB$,$\angle BAP=180^\circ - \angle BAC=160^\circ$,则$\angle ABP=(180^\circ - 160^\circ)÷2=10^\circ$;
点$P$在$A$右侧:$\angle ABP=\angle APB$,$\angle BAP=20^\circ$,则$\angle ABP=(180^\circ - 20^\circ)÷2=80^\circ$。
2. 当$BA=BP$时,
点$P$在$A$右侧:$\angle BAP=\angle BPA=20^\circ$,则$\angle ABP=180^\circ - 20^\circ - 20^\circ=140^\circ$;
点$P$在$A$左侧:$\angle BPA=\angle BAP$,$\angle BAP=180^\circ - 20^\circ=160^\circ$,此时$\angle BPA=160^\circ$,不成立(三角形内角和大于$180^\circ$)。
3. 当$PA=PB$时,
点$P$在$A$右侧:$\angle PAB=\angle PBA=20^\circ$,则$\angle ABP=20^\circ$;
点$P$在$A$左侧:$\angle PAB=\angle PBA$,$\angle PAB=180^\circ - 20^\circ=160^\circ$,此时$\angle PBA=160^\circ$,不成立(三角形内角和大于$180^\circ$)。
综上,$\angle ABP$大小是$10^\circ$或$20^\circ$或$80^\circ$或$140^\circ$。
$10^\circ$或$20^\circ$或$80^\circ$或$140^\circ$
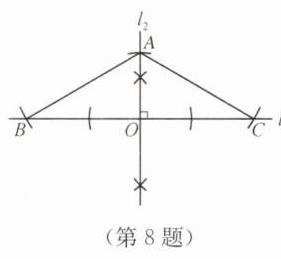
8. 如图,已知线段$a$,$b$,求作等腰三角形,使其底边长为$b$,底边上的高为$a$(不写作法,保留作图痕迹). 能否作出腰长为$b$,腰上的高为$a$的三角形?试试看.

答案:如图,先作两条互相垂直的直线$l_1,l_2$,交于点O,在射线OA上取线段$OA=a$,以A为圆心,取$AB=b,AC=b$,其中点B,C在直线$l_1$上,连接点A,B,C。$\triangle ABC$即为所求。不能作出腰长为b,腰上的高为a的三角形