2025年同步练习江苏八年级数学上册苏科版第23页解析答案

8. 如图,在四边形$ABCD$中,对角线$BD平分\angle ABC$,且$\angle BAD与\angle BCD$互补. 求证：$AD = CD$.

答案：
如图，过点 D 作 DE⊥AB,交 BA 的延长线于点 E,作 DF⊥BC,垂足为 F.
∵ BD 平分∠ABC,
∴ DE=DF.
∵ ∠BAD 与∠BCD 互补,∠EAD+∠BAD=180°,
∴ ∠DAE=∠C.在△ADE 和△CDF 中,∠DAE=∠C,∠E=∠DFC,DE=DF,
∴ △ADE≌△CDF(AAS).
∴ AD=CD.

9. 如图,在$\triangle ABC$中,$\angle B = 60^\circ$,$AD$,$CE分别是\angle BAC$,$\angle BCA$的平分线,$AD$,$CE相交于点F$. 求证：$FE = FD$.

答案：
如图，过点 F 作 FM⊥AB,垂足为 M.作 FN⊥BC,垂足为 N,连接 BF.
∵ F 是角平分线的交点,
∴ BF 也是角平分线,
∴ MF=FN.
∵ ∠ABC=60°,
∴ ∠MFN=180° - ∠ABC=120°.
∵ ∠CFA=180°-(∠FAC+∠FCA)=180° - $\frac{1}{2}$(∠ABC+∠ACB)=180° - $\frac{1}{2}$(180° - ∠ABC)=180° - $\frac{1}{2}$(180° - 60°)=120°,
∴ ∠DFE=∠CFA=∠MFN=120°.
∵ ∠MFD + ∠DFN=∠DFN + ∠NFE,
∴ ∠DFM=∠NFE.在△DMF 和△ENF 中,∠DMF=∠ENF,MF=NF,∠DFN=∠NFE,
∴ △DMF≌△ENF(ASA).
∴ FE=FD

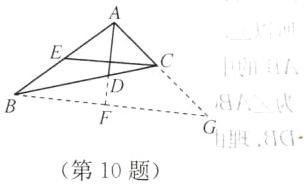
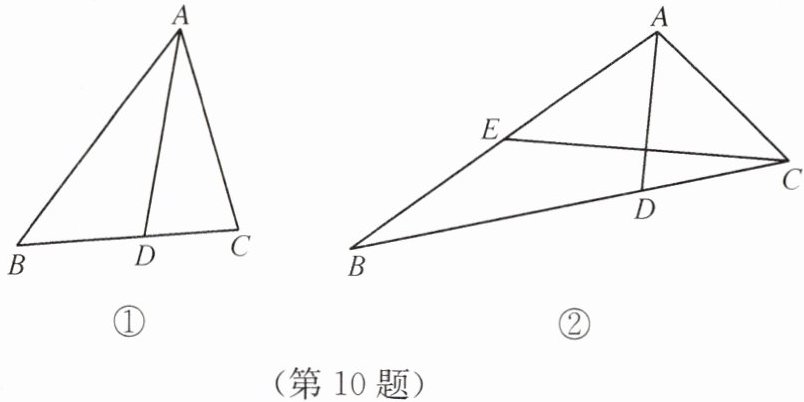
10. 某数学兴趣小组进行如下探究：如图①,在$\triangle ABC$中,$AD$是角平分线,此时角平分线不一定平分三角形的面积,但发现$\triangle ABD和\triangle ACD$的面积比等于图中两组不同的线段比.
(1)如图①,$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}= $______,$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}= $______.(填两个不同的答案)
(2)【得出结论】$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}= $______= ______；
(3)【应用结论】如图②,在$\triangle ABC$中,$AD$是角平分线,$BD = 2CD$,$E是边AB$的中点,连接$CE$.
① 求证：$AD垂直平分CE$；
② 若$\triangle ABD的边AD上的高为BF$,求$\frac{S_{\triangle BDF}}{S_{\triangle ACD}}$.

答案：

(1)$\frac{AB}{AC}$,$\frac{BD}{CD}$
(2)$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{AB}{AC}=\frac{BD}{CD}$
(3)①
∵ BD=2CD,
∴ $\frac{BD}{CD}$=2.由
(1)知,$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{AB}{AC}=\frac{BD}{CD}$=2,
∴ AB=2AC.
∵ E 为 AB 的中点,
∴ AB=2AE,
∴ AC=AE,
∴ AD 垂直平分 CE ② 如图，过点 B 作 AD 的垂线，与 AD 的延长线交于点 F,延长 AC,BF 交于点 G,设△ACD 的面积=x,△BDF 的面积=y.
∵ BD=2CD,
∴ S△ABD=2S△ACD=2x,
∴ S△ABF=2x + y.
∵ AD 平分∠BAC,
∴ ∠BAF=∠CAF.
∵ BF⊥AF,
∴ ∠AFB=∠AFG=90°.
∵ AF=AF,
∴ △AFB≌△AFG(ASA),
∴ S△ABF=S△AFG=2x + y,AB=AG,
∴ S四边形CDFG=S△AFG - S△ACD=2x + y - x=x + y.由①得 AB=2AE=2AC,
∴ AG=2AC,
∴ AC=CG,
∴ S△ADC=S△DGC,
∴ x + 2x=y + x + y,
∴ x=y,
∴ $\frac{S_{\triangle BDF}}{S_{\triangle ACD}}=\frac{y}{x}$=1