1. 三角形全等的判定方法有
SAS,ASA,AAS,SSS
,全等三角形的性质有
全等三角形的对应边相等、对应角相等
.
答案:SAS,ASA,AAS,SSS;全等三角形的对应边相等、对应角相等
2. 如图,已知∠B= ∠E,AB= DE,要想推出△ABC≌△DEC:
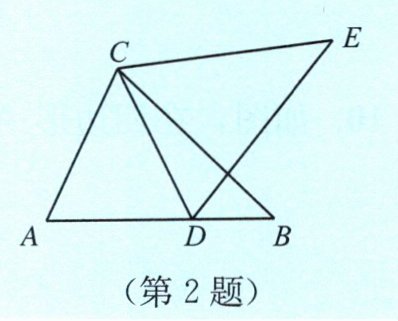
(1)若以“SAS”为依据,则需要添加条件______
BC=EC
;
(2)若以“ASA”为依据,则需要添加条件______
∠A=∠CDE
;
(3)若以“AAS”为依据,则需要添加条件______
∠ACB=∠DCE
.
答案:(1)BC=EC;(2)∠A=∠CDE;(3)∠ACB=∠DCE
3. 在△ABC和△DEF中,给出下列四组条件:
①AB= DE,BC= EF,AC= DF;②AB= DE,∠B= ∠E,BC= EF;
③∠B= ∠E,BC= EF,∠C= ∠F;④∠A= ∠D,∠B= ∠E,∠C= ∠F.
其中,能使△ABC≌△DEF的条件共有(
C
)
A.1组
B.2组
C.3组
D.4组
答案:C
解析:
①AB=DE,BC=EF,AC=DF,符合SSS,能判定△ABC≌△DEF;
②AB=DE,∠B=∠E,BC=EF,符合SAS,能判定△ABC≌△DEF;
③∠B=∠E,BC=EF,∠C=∠F,符合ASA,能判定△ABC≌△DEF;
④∠A=∠D,∠B=∠E,∠C=∠F,仅三角对应相等,不能判定△ABC≌△DEF。
能使△ABC≌△DEF的条件共有3组。
C
4. 如图,∠BAC= ∠DAC,添加一个条件后,仍无法判定△ABC≌△ADC的是(
B
)
A.AB= AD
B.CB= CD
C.∠BCA= ∠DCA
D.∠B= ∠D= 90°
答案:B
5. 如图,在△ABC和△DEF中,点A,E,B,D在同一条直线上,AC//DF,AC= DF,只添加一个条件,能判定△ABC≌△DEF的是(
B
)
A.BC= EF
B.AE= DB
C.∠A= ∠D
D.∠ABC= ∠D
答案:B
解析:
∵AC//DF,
∴∠A=∠D。
∵AC=DF,
若添加条件AE=DB,
∵点A,E,B,D在同一条直线上,
∴AE+EB=DB+EB,即AB=DE。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AC=DF\\ ∠A=∠D\\ AB=DE\end{array}\right.$,
∴△ABC≌△DEF(SAS)。
B
6. 根据下列已知条件,能画出唯一△ABC的是(
D
)
A.AB= 5,BC= 3,AC= 8
B.AB= 4,BC= 3,∠A= 30°
C.∠C= 90°,AB= 6
D.∠A= 60°,∠B= 45°,AB= 4
答案:D
解析:
A. $AB + BC = 5 + 3 = 8 = AC$,不能构成三角形。
B. 已知两边及其中一边的对角,三角形不唯一。
C. 已知直角和斜边,直角边长度不确定,三角形不唯一。
D. 两角及其夹边确定,三角形唯一。
D
7. 如图,在四边形ABCD中,AB//CD,AC与BD相交于点O,且OA= OC. 猜想边AD与边BC的关系,并加以证明.

答案:AD//BC. 证明:如图,
∵AB//CD,
∴∠1=∠2.在△AOB 和△COD 中,$\left\{\begin{array}{l} ∠1=∠2,\\ OA=OC,\\ ∠3=∠4,\end{array}\right. $
∴ △AOB≌△COD(ASA).
∴ OB=OD. 在△AOD 和△COB 中,$\left\{\begin{array}{l} OA=OC,\\ ∠5=∠6,\\ OB=OD,\end{array}\right. $
∴△AOD≌△COB(SAS).
∴AD=BC,∠DAO=∠BCO,
∴AD//BC
