8. 如图,在△ABD与△AEC中,AB= AD= BD,AE= AC= EC,∠DAB= ∠EAC= 60°,AB≠AC,连接BE,CD相交于点O.
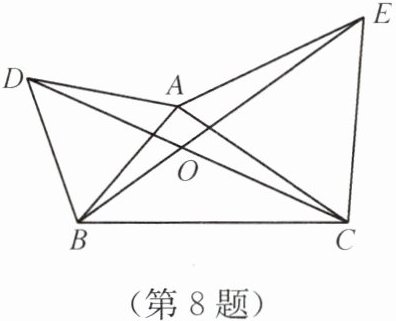
(1)求证:BE= DC;
(2)求证:∠BOD= 60°.
答案:(1)如图,
∵AD=AB,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE.在△ADC 和△ABE 中,$\left\{\begin{array}{l} AD=AB,\\ ∠DAC=∠BAE,\\ AC=AE,\end{array}\right. $
∴△ADC≌△ABE(SAS).
∴BE=DC
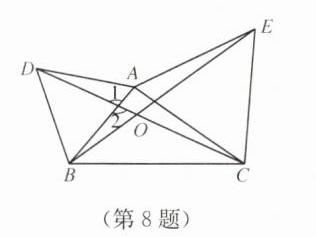
(2)
∵△ADC≌△ABE(SAS),
∴∠ADC=∠ABE.
∵∠1=∠2,
∴∠ADC+∠DAB=∠ABE+∠DOB.
∵∠DAB=60°,
∴∠DOB=∠DAB=60°
9. 如图,AC,BD相交于点O,且AB//CD,AB= CD,点E,F分别是OA,OC的中点,连接DF,BE. 求证:DF= BE.

答案:
∵AB//CD,
∴∠A=∠C.在△AOB 和△COD 中,$\left\{\begin{array}{l} ∠AOB=∠COD,\\ ∠A=∠C,\\ AB=CD,\end{array}\right. $
∴△AOB≌△COD(AAS).
∴OA=OC,OB=OD.
∵点 E,F 分别是 OA,OC 的中点,
∴OF=$\frac {1}{2}$OA,OE=$\frac {1}{2}$OC,
∴OF=OE.在△DOF 和△BOE 中,$\left\{\begin{array}{l} OF=OE,\\ ∠DOF=∠BOE,\\ OB=OD,\end{array}\right. $
∴△DOF≌△BOE(SAS).
∴DF=BE
10. 在△ABC和△A′B′C′中,∠B= ∠B′= 30°,AB= A′B′= 6,AC= A′C′= 4. 已知∠C= 70°,求∠C′的度数.
答案:如图①,当△ABC≌△A'B'C'时,∠C'=∠C=70°;如图②,当△ABC 与△A'B'C'不全等时,取 CC'的中点 D,连接AD,证明△ADC≌△ADC',所以∠AC'C=∠C=70°,所以∠AC'B=180°-70°=110°.综上∠A'C'B'为70°或110°
解析:
情况一:当△ABC≌△A'B'C'时,∠C'=∠C=70°。
情况二:当△ABC与△A'B'C'不全等时,在△ABC和△A'B'C'中,∠B=∠B'=30°,AB=A'B'=6,AC=A'C'=4。以A为圆心,AC长为半径画弧,交BC于C和另一点C''(C''与C不重合),则AC''=AC=4。连接AC'',则△ABC''满足条件。在△ACC''中,AC=AC''=4,过A作AD⊥BC于D,则AD平分∠CAC'',CD=C''D。∠C=70°,则∠ACB=70°,∠ACC''=70°,所以∠AC''B=180°-∠ACC''=110°,即∠C'=110°。
综上,∠C'的度数为70°或110°。
