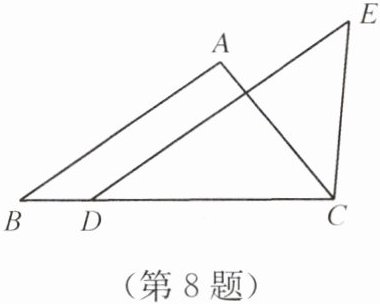
8. 如图,在$\triangle ABC$中,点$D在边BC$上,$CE= AC$,$DE// AB$,$\angle DCE= \angle A$. 求证:$DE= BC$.
答案:
∵ DE//AB,
∴ ∠B=∠EDC.在△ABC和△CDE中,CE=AC,∠A=∠DCE,∠B=∠EDC,
∴ △ABC≌△CDE(AAS).
∴ DE=BC
9. 如图,在$\triangle ABC$中,$\angle C= 90^\circ$,点$D在边AB$上,$DF\perp AB$,垂足为$D$,$DF= AC$,过点$F作FE// BC$,交$AB于点E$. 求证:$DE= BC$.

答案:
∵ DF⊥AB,
∴ ∠FDE=90°,
∴ ∠FDE=∠C=90°.
∵ FE//BC,
∴ ∠FED=∠B.在△ABC和△FED中,∠B=∠FED,∠C=∠FDE,AC=DF,
∴ △ABC≌△FED(AAS).
∴ DE=BC
10. 如图,$\angle AOB= 90^\circ$,$OA= OB$,直线$l经过点O$,过点$A作AC\perp l$,垂足为$C$,过点$B作BD\perp l$,垂足为$D$. 求证:$BD+CD= AC$.

答案:如图,
∵ ∠AOB=90°,
∴ ∠1+∠2=90°.
∵ AC⊥l,BD⊥l,
∴ ∠ACO=∠ODB=90°,
∴ ∠2+∠B=90°,
∴ ∠1=∠B.在△ACO和△ODB中,∠ACO=∠ODB,∠1=∠B,OA=OB,
∴ △ACO≌△ODB(AAS).
∴ AC=OD,OC=BD.
∴ BD+CD=OC+CD=OD,
∴ BD+CD=AC