1. 两角分别相等且其中一组等角的
对边
相等的两个三角形全等(简称“角角边”或“AAS”).
答案:对边
2. 如图,$BC= EC$,$\angle BCE= \angle ACD$,要使$\triangle ABC\cong\triangle DEC$,则应添加的一个与角有关的条件为
∠A=∠D(或∠B=∠E)
.(答案不唯一,只需填一个)
答案:∠A=∠D(或∠B=∠E)
3. 如图,点$P在\angle AOB$的平分线上,$PE\perp OA$,垂足为$E$,$PF\perp OB$,垂足为$F$,若$PE= 4$,则$PF= $
4
.
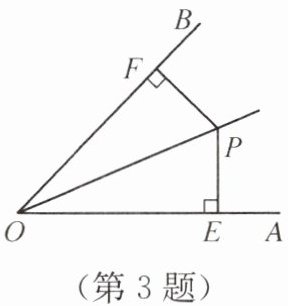
答案:4
解析:
∵点$P$在$\angle AOB$的平分线上,$PE\perp OA$,$PF\perp OB$,
∴$PF = PE$(角平分线上的点到角两边的距离相等)。
∵$PE = 4$,
∴$PF = 4$。
4
4. 下列说法中正确的是(
D
)
A.斜边相等的两个直角三角形全等
B.底边相等的两个等腰三角形全等
C.两个等边三角形全等
D.腰相等的两个等腰直角三角形全等
答案:D
5. 能判定$\triangle ABC\cong\triangle A'B'C'$的条件是(
D
)
A.$AB= A'B'$,$AC= A'C'$,$\angle B= \angle B'$
B.$AB= A'B'$,$\angle A= \angle A'$,$\angle B= \angle C'$
C.$\angle A= \angle A'$,$\angle B= \angle B'$,$\angle C= \angle C'$
D.$AC= A'C'$,$\angle B= \angle B'$,$\angle C= \angle C'$
答案:D
解析:
A. $AB= A'B'$,$AC= A'C'$,$\angle B= \angle B'$,SSA不能判定全等;
B. $AB= A'B'$,$\angle A= \angle A'$,$\angle B= \angle C'$,对应角不相等,不能判定全等;
C. $\angle A= \angle A'$,$\angle B= \angle B'$,$\angle C= \angle C'$,AAA不能判定全等;
D. $AC= A'C'$,$\angle B= \angle B'$,$\angle C= \angle C'$,AAS能判定全等。
D
6. 如图,在$\triangle ABC$中,$\angle ABC= 45^\circ$,$AC= 8$,高$AD和BE交于点F$,则$BF$的长为(
C
)

A.4
B.6
C.8
D.9
答案:C
解析:
∵AD,BE是△ABC的高,
∴∠ADB=∠ADC=∠BEC=90°,
∵∠ABC=45°,
∴∠BAD=45°=∠ABC,
∴AD=BD,
∵∠AFE=∠BFD,∠AEF=∠BDF=90°,
∴∠CAD=∠FBD,
在△ADC和△BDF中,
$\left\{\begin{array}{l} ∠CAD=∠FBD\\ AD=BD\\ ∠ADC=∠BDF\end{array}\right.$,
∴△ADC≌△BDF(ASA),
∴BF=AC=8.
C
7. 如图,$AB= AE$,$\angle 1= \angle 2$,$\angle C= \angle D$. 求证:$\triangle ABC\cong\triangle AED$.

答案:
∵ ∠1=∠2,
∴ ∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD.在△ABC和△AED中,∠C=∠D,∠BAC=∠EAD,AB=AE,
∴ △ABC≌△AED(AAS)