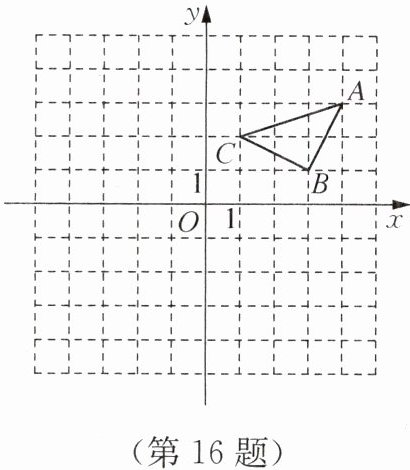
16. 在10×10的正方形网格中,建立如图所示的平面直角坐标系$,△A_1B_1C_1$是由△ABC平移后得到的,且△ABC中任意一点P(x,y)经过平移后的对应点为$P_1(x-4,y+2).$
(1)在图中画出$△A_1B_1C_1,$点$A_1$的坐标为
(0,5)
;
$(2)△A_1B_1C_1$的面积为
$\frac{5}{2}$
;
(3)在y轴上作点Q,使$QB_1+QC_1$的值最小;
(4)若点M在y轴上$,△MOC_1$的面积为6,则点M的坐标为
(0,4)或(0,-4)
.
答案:
(1)(0,5)
(2)$\frac{5}{2}$
(3)略
(4)(0,4)或(0,-4)
17. 如图,已知点A,C的坐标分别为(-1,0),(1,4),点B在x轴上,且AB= 3.
(1)求点B的坐标.
(2)求△ABC的面积.
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.

答案:
(1)点B在点A右边时,点B的坐标为(2,0);点B在点A左边时,点B的坐标为(-4,0)
(2)6
(3)(0,$\frac{20}{3}$)或(0,$-\frac{20}{3}$)
18. 如图,将一张长方形纸片ABCF放在平面直角坐标系中,点F与原点O重合,点A在x轴的正半轴上,点C在y轴的正半轴上,OA= 10,OC= 8.在边OC上取一点D,将纸片沿AD翻折,使点F恰好落在边BC上的点E处,求D,E两点的坐标.

答案:根据四边形OABC是长方形,OA=10,OC=8,可知∠B=∠OCB=90°,BC=OA=10,AB=OC=8,由翻折得AE=OA=10,DE=OD.在Rt△ABE中,由勾股定理,得BE=6,所以CE=4,所以点E的坐标为(4,8).设DE=OD=y,则CD=OC-OD=8-y.在Rt△CDE中,由勾股定理,得CD²+CE²=DE²,所以(8-y)²+4²=y²,解得y=5.所以OD=5,所以点D的坐标为(0,5)
解析:
∵四边形OABC是长方形,OA=10,OC=8,
∴∠B=∠OCB=90°,BC=OA=10,AB=OC=8。
由翻折得AE=OA=10,DE=OD。
在Rt△ABE中,$BE=\sqrt{AE^2 - AB^2}=\sqrt{10^2 - 8^2}=6$,
∴CE=BC - BE=10 - 6=4,
∴点E的坐标为(4,8)。
设DE=OD=y,则CD=OC - OD=8 - y。
在Rt△CDE中,$CD^2 + CE^2 = DE^2$,
即$(8 - y)^2 + 4^2 = y^2$,
解得y=5。
∴OD=5,
∴点D的坐标为(0,5)。