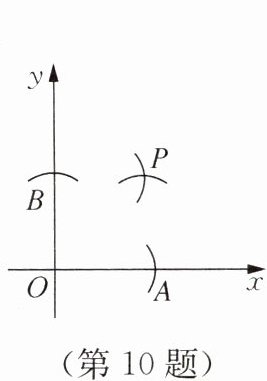
10. 如图,在x轴、y轴上分别截取OA,OB,使OA= OB,再分别以点A,B为圆心,以大于AB一半的长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为______
3
.
答案:3
解析:
由题意知,点P在∠AOB的角平分线上,所以点P到x轴和y轴的距离相等,即|a|=|2a-3|。
因为点P在第一象限(由图可知),所以a>0,2a-3>0,即a=2a-3,解得a=3。
3
11. 在平面直角坐标系中,点P(m-1,m+2)在第二象限,且点P到y轴的距离是1,则点P的坐标为
(-1,2)
.
答案:(-1,2)
解析:
∵点P(m-1,m+2)在第二象限,
∴m-1<0,m+2>0,
∵点P到y轴的距离是1,
∴|m-1|=1,
又
∵m-1<0,
∴m-1=-1,解得m=0,
∴m+2=0+2=2,
∴点P的坐标为(-1,2)。
12. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转90°得到线段AC.若点C的坐标为(m,4),则点B的坐标为______
(3,0)
.
答案:(3,0)
解析:
过点C作CD⊥y轴于点D,垂足为D。
∵点A的坐标为(0,1),点C的坐标为(m,4),
∴CD=m,OD=4,OA=1,AD=OD-OA=4-1=3。
∵线段AB绕点A按逆时针方向旋转90°得到线段AC,
∴AB=AC,∠BAC=90°,
∴∠OAB+∠CAD=90°。
∵CD⊥y轴,
∴∠CDA=90°,∠ACD+∠CAD=90°,
∴∠OAB=∠ACD。
在△AOB和△CDA中,
∠AOB=∠CDA=90°,∠OAB=∠ACD,AB=CA,
∴△AOB≌△CDA(AAS),
∴OB=AD=3,OA=CD=1,
∴点B的坐标为(3,0)。
(3,0)
13. 在平面直角坐标系中,对于平面内任意一点(x,y),规定以下两种变化:①f(x,y)= (-x,y),②g(x,y)= (x,x-y).按照该规定:f(g(-1,2))=
(1,-3)
.
答案:(1,-3)
解析:
先计算$g(-1,2)$,根据$g(x,y)=(x,x - y)$,可得$g(-1,2)=(-1,-1 - 2)=(-1,-3)$。
再计算$f(g(-1,2))=f(-1,-3)$,根据$f(x,y)=(-x,y)$,可得$f(-1,-3)=( -(-1),-3)=(1,-3)$。
$(1,-3)$
14. 如图,在平面直角坐标系中,Rt△ABC的顶点A在x轴上,顶点B在y轴上,∠ACB= 90°,OB//AC,点C的坐标为(1,2),点D和点C关于AB成轴对称,且AD交y轴于点E.点E的坐标为
(0,$\frac{3}{4}$)
.
答案:(0,$\frac{3}{4}$)
解析:
∵点$C$的坐标为$(1,2)$,$OB// AC$,$\angle ACB = 90^\circ$,
∴点$B$的横坐标为$0$,纵坐标与$C$相同为$2$,即$B(0,2)$;$AC$垂直于$BC$,$AC$平行于$y$轴,所以点$A$的纵坐标为$0$,横坐标与$C$相同为$1$,即$A(1,0)$。
设直线$AB$的解析式为$y = kx + b$,将$A(1,0)$,$B(0,2)$代入得:
$\begin{cases}k + b = 0 \\ b = 2\end{cases}$,解得$\begin{cases}k = -2 \\ b = 2\end{cases}$,
∴直线$AB$的解析式为$y=-2x + 2$。
设点$D$的坐标为$(m,n)$,
∵点$D$和点$C(1,2)$关于$AB$成轴对称,
∴线段$CD$的中点$\left(\dfrac{m + 1}{2},\dfrac{n + 2}{2}\right)$在直线$AB$上,且直线$CD$与直线$AB$垂直。
直线$AB$的斜率为$-2$,所以直线$CD$的斜率为$\dfrac{1}{2}$,即$\dfrac{n - 2}{m - 1}=\dfrac{1}{2}$,$2(n - 2)=m - 1$,$m = 2n - 3$。
中点$\left(\dfrac{m + 1}{2},\dfrac{n + 2}{2}\right)$代入$y=-2x + 2$得:
$\dfrac{n + 2}{2}=-2×\dfrac{m + 1}{2}+ 2$,$n + 2=-2(m + 1)+ 4$,$n + 2=-2m - 2 + 4$,$n + 2=-2m + 2$,$n=-2m$。
将$m = 2n - 3$代入$n=-2m$得:$n=-2(2n - 3)$,$n=-4n + 6$,$5n = 6$,$n=\dfrac{6}{5}$,$m = 2×\dfrac{6}{5}- 3=\dfrac{12}{5}-\dfrac{15}{5}=-\dfrac{3}{5}$,
∴点$D\left(-\dfrac{3}{5},\dfrac{6}{5}\right)$。
设直线$AD$的解析式为$y = k_1x + b_1$,将$A(1,0)$,$D\left(-\dfrac{3}{5},\dfrac{6}{5}\right)$代入得:
$\begin{cases}k_1 + b_1 = 0 \\ -\dfrac{3}{5}k_1 + b_1=\dfrac{6}{5}\end{cases}$,
两式相减得:$\dfrac{8}{5}k_1=-\dfrac{6}{5}$,$k_1=-\dfrac{3}{4}$,$b_1=-k_1=\dfrac{3}{4}$,
∴直线$AD$的解析式为$y=-\dfrac{3}{4}x + \dfrac{3}{4}$。
令$x = 0$,则$y=\dfrac{3}{4}$,
∴点$E$的坐标为$\left(0,\dfrac{3}{4}\right)$。
$\left(0,\dfrac{3}{4}\right)$
15. 如图,智能机器人的行走路径是梯形ABCD,其中AB//CD,BC⊥AB,AB= 5,BC= 4,CD= 3.在原图中建立适当的平面直角坐标系,并写出各顶点的坐标.

答案:答案不唯一.例:以AB所在直线为x轴,BC所在直线为y轴建立平面直角坐标系,则坐标为A(-5,0),B(0,0),C(0,4),D(-3,4)