2025年同步练习江苏八年级数学上册苏科版第124页解析答案

17. 如图,公路MN和公路PQ在点P处交汇,公路PQ边的A处有一栋居民楼,点A到公路MN的距离为80 m,现有一卡车在公路MN上以5 m/s的速度沿PN方向行驶,卡车行驶时周围100 m以内都会受到噪声的影响,该居民楼受卡车噪声影响的时间有多长？

答案：
如图,设卡车开到C处居民楼开始受到影响，行驶到D处时居民楼受噪声的影响结束，则有CA=DA=100m;在Rt△ABC中,$CB=\sqrt{100^2 - 80^2}=60$(m),
∴CD=2CB=120m.所以该居民楼受影响的时间为120÷5=24(s)

18. 勾股定理的证法多样. 当两个全等的直角三角形按如图方式摆放时,可以证明勾股定理$a^{2}+b^{2}= c^{2}$,图中$\angle BAD= 90^{\circ}$,四边形ACFE是正方形. 请你用该图证明勾股定理.

答案：四边形ACFD的面积=$\frac{1}{2}(AC + DF)\cdot CF=\frac{1}{2}(b + b + a)\cdot b=b^2+\frac{ab}{2}$,BF=b - a.
∵$S_{四边形ABED}=S_{\triangle ABE}+S_{\triangle ADE}=\frac{1}{2}b^2+\frac{1}{2}ab$,$S_{四边形ABED}=S_{\triangle ADB}+S_{\triangle DEB}=\frac{1}{2}c^2+\frac{1}{2}a(b - a)$,
∴$\frac{1}{2}b^2+\frac{1}{2}ab=\frac{1}{2}c^2+\frac{1}{2}a(b - a)$,
∴$a^2 + b^2=c^2$

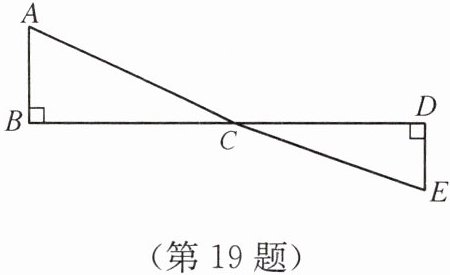
19. 如图,C为线段BD上的一个动点,分别过点B,D作AB⊥BD,ED⊥BD,垂足分别为B,D,连接AC,EC. 已知AB= 3,DE= 2,BD= 12,设CD= x.
(1)用含x的代数式表示AC+CE的长.
(2)求点C满足什么条件时,AC+CE的值最小,并求出此时AC+CE的最小值.
(3)根据(2)中的规律和结论,重新构图求代数式$\sqrt{x^{2}+1}+\sqrt{(8-x)^{2}+25}$的最小值.

答案：

(1)
∵AB⊥BD,AB=3,CD=x,
∴BC=12 - x.在Rt△ABC中,$AC=\sqrt{AB^2 + BC^2}=\sqrt{9+(12 - x)^2}$.
∵ED⊥BD,DE=2,在Rt△DEC中,$CE=\sqrt{CD^2 + DE^2}=\sqrt{x^2 + 4}$,
∴$AC + CE=\sqrt{9+(12 - x)^2}+\sqrt{x^2 + 4}$
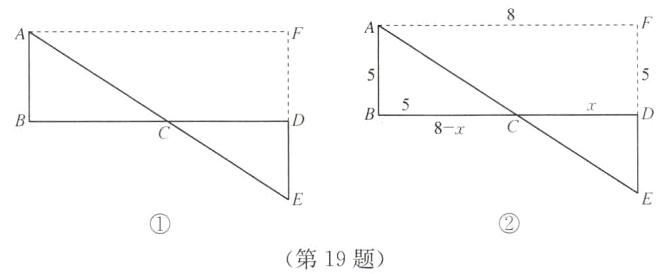
(2)如图①,当C是AE和BD交点时，过点D作DF⊥BD，过点A作AF⊥AB，
∴$AC + CE=AE=\sqrt{AF^2 + EF^2}=\sqrt{12^2 + 5^2}=13$,
∴AC + CE的最小值为13
(3)如图②,由
(2),使AB=5,ED=1,DB=8,连接AE交BD于点C,
∴$AE=AC + CE=\sqrt{(8 - x)^2+25}+\sqrt{x^2 + 1}$,
∴AE的长即为代数式$\sqrt{x^2 + 1}+\sqrt{(8 - x)^2+25}$最小值.
∵四边形ABDF为长方形，
∴AB=DF=5,AF=BD=8.在Rt△AEF中,由勾股定理,得$AE=\sqrt{AF^2 + EF^2}=\sqrt{8^2 + 6^2}=10$