14. 已知△ABC的三边分别为a,b,c,且a+b= 3,ab= 1,c= $\sqrt{7}$.
(1)求$a^{2}+b^{2}$的值;
(2)试判断△ABC的形状,并说明理由.
答案:
(1)
∵a + b=3,ab=1,
∴$a^2 + b^2=(a + b)^2-2ab=9 - 2=7$
(2)△ABC是直角三角形,理由:
∵$a^2 + b^2=7$,$c^2=(\sqrt{7})^2=7$,
∴$a^2 + b^2=c^2$,
∴△ABC是直角三角形
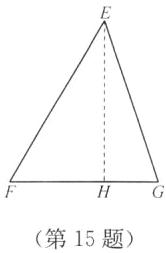
15. 如图,在△EFG中,EF= 15,FG= 14,EG= 13,求△EFG的面积.
答案:如图,过点E作EH⊥FG,垂足为H.在Rt△EFH和Rt△EGH中,由勾股定理,得$EH^2=EF^2 - FH^2$,$EH^2=EG^2 - GH^2$,
∴$EG^2 - GH^2=EF^2 - FH^2$.设FH=x,则GH=14 - x.
∵EF=15,FG=14,EG=13,
∴$13^2-(14 - x)^2=15^2 - x^2$,解得x=9.
∴$EH=\sqrt{15^2 - 9^2}=12$,
∴$S_{\triangle EFG}=\frac{1}{2}× FG\cdot EH=\frac{1}{2}×14×12=84$,
∴△EFG的面积为84
16. 如图,某实践探究小组在放风筝时想测量风筝离地面的竖直高度,通过测量,得到手和风筝的水平距离BC的长为15 m,手到地面的距离为1.7 m. 根据手中剩余线的长度计算出风筝线AB的长为17 m.
(1)求风筝的高度AD.
(2)如果想要风筝沿DA方向再上升12 m,BC的长度保持不变,则放风筝者应该再放出多少米的风筝线?

答案:
(1)在Rt△ABC中,∠ACB=90°,BC=15,AB=17,由勾股定理,得$AC=\sqrt{AB^2 - BC^2}=\sqrt{17^2 - 15^2}=8$,则AD=AC + CD=8 + 1.7=9.7(m)
(2)风筝沿DA方向再上升12m后,风筝的高度为20m,此时风筝线的长为$\sqrt{20^2 + 15^2}=25$(m),25 - 17=8(m).他应该再放出8m长的线