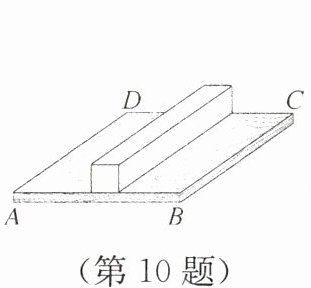
10. 如图,在长方形桌面ABCD上放着一根长方体木块,已知AD= 6 m,AB= 5 m,该木块的较长边与AD平行,横截面是边长为1 m的正方形,一只蚂蚁从点A出发爬过木块到达C处,爬行的最短路程是______m.
答案:$\sqrt{85}$
解析:
将木块上方平面展开与桌面平面形成一个新的长方形,长为 $AB + 2 × 1 = 5 + 2 = 7\ m$,宽为 $AD = 6\ m$。蚂蚁爬行的最短路程为该长方形对角线长,即 $\sqrt{7^2 + 6^2} = \sqrt{49 + 36} = \sqrt{85}\ m$。
$\sqrt{85}$
11. 如图,在△ABC中,AB= AC,BC= 4,△ABC的面积是14,AC的垂直平分线EF分别交边AC,AB于点E,F. 若D为边BC的中点,M为线段EF上的一个动点,则△CDM周长的最小值是
9
.
答案:9
解析:
连接AD,AM。
∵AB=AC,D为BC中点,BC=4,
∴AD⊥BC,BD=CD=2。
∵S△ABC=14,
∴$\frac{1}{2} × BC × AD = 14$,即$\frac{1}{2} × 4 × AD = 14$,解得AD=7。
∵EF垂直平分AC,
∴MA=MC。
△CDM周长=CD+DM+MC=CD+DM+MA。
当A,M,D共线时,DM+MA最小,最小值为AD=7。
∴△CDM周长最小值=2+7=9。
9
12. 如图,在Rt△ABC中,$\angle ACB= 90^{\circ}$,AC= 8,BC= 6,CD⊥AB,垂足为D.
(1)求斜边AB的长;
(2)求△ABC的面积;
(3)求高CD.

答案:
(1)
∵在Rt△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{AC^2+BC^2}$=10
(2)△ABC的面积=$\frac{1}{2}AC\cdot BC=\frac{1}{2}×6×8=24$
(3)由
(2)可知,$\frac{1}{2}AC\cdot BC=\frac{1}{2}CD\cdot AB=24$,
∴CD=4.8
13. 如图,在△ABC中,$\angle C= 90^{\circ}$,AC= 4,BC= 8.
(1)用直尺和圆规作AB的垂直平分线;(保留作图痕迹,不要求写作法)
(2)若(1)中所作的垂直平分线交BC于点D,求BD的长.

答案:(1)如图,直线MN即为所求

(2)
∵MN垂直平分线段AB,
∴DA=DB.设DA=DB=x,在Rt△ACD中,
∵$AD^2=AC^2+CD^2$,
∴$x^2=4^2+(8 - x)^2$,解得x=5,
∴BD=5