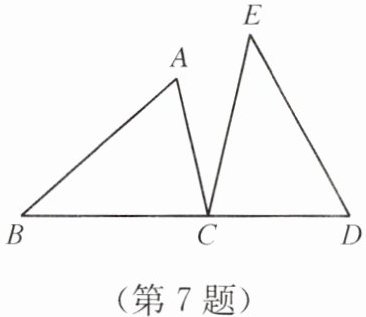
7. 如图,点 C 在线段 BD 上,在△ABC 和△DEC 中,∠A= ∠D,AB= DE,∠B= ∠E. 求证:AC= DC.
答案:在△ABC和△DEC中,∠A=∠D,AB=DE,∠B=∠E,
∴△ABC≌△DEC(ASA).
∴AC=DC
8. 如图,已知点 E,F 在 AC 上,AD//CB,且 AD= CB,∠D= ∠B. 求证:AE= CF.

答案:
∵AD//CB,
∴∠A=∠C.在△ADF和△CBE中,AD=CB,∠A=∠C,∠D=∠B,
∴△ADF≌△CBE(ASA).
∴AF=CE,
∴AF+EF=CE+EF,即AE=CF
9. 如图,在 Rt△ABC 中,∠ABC= 90°,点 D 在 BC 的延长线上,且 BD= AB,过点 B 作 BE⊥AC,与 BD 的垂线 DE 交于点 E. 求证:AC= BE.

答案:令AC与BE交于点F
∵∠ABC=90°,
∴∠A+∠ACB=90°.
∵BE⊥AC,
∴∠BFC=90°,
∴∠FBC+∠ACB=90°,
∴∠A=∠DBE.
在△ABC和△EDB中,
∠A=∠DBE,AB=BD,∠ABC=∠D=90°,
∴△ABC≌△EDB(ASA).
∴AC=BE
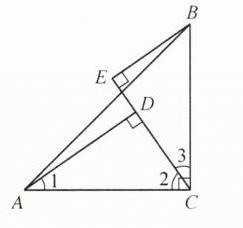
10. 如图,在 Rt△ABC 中,∠ACB= 90°,AC= BC,AD⊥CE,BE⊥CE,垂足分别为 D,E. 求证:AD-BE= DE.

答案:如图$,$
∵$AD⊥CE,BE⊥CE,$
∴$∠ADC=∠CEB=90°,$
∴$∠1+∠2=90°.$
∵$∠ACB=90°,$
∴$∠2+∠3=90°,$
∴$∠1=∠3,$
∴$∠2=∠EBC.$
在$△ADC$和$△CEB$中$,$
$∠1=∠3,$
$∠2=∠EBC,$
$AC=BC,$
∴$△ADC≌△CEB(ASA).$
∴$AD=CE,CD=BE,$
∴$CE - CD=DE,$即$AD - BE=DE$