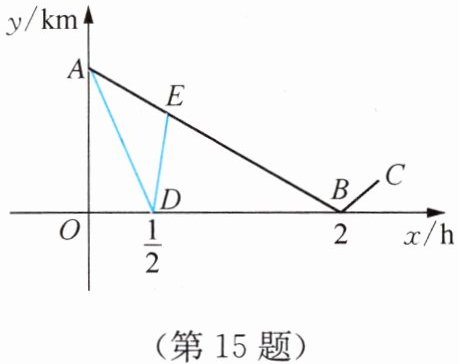
15. 甲、乙两人从相距4 km的两地同时、同向出发,乙每小时走4 km,一只小狗随甲一起同向出发,小狗追上乙时它就往甲这边跑,遇到甲时又往乙这边跑,遇到乙时再往甲这边跑……就这样一直匀速跑下去.如图,折线A—B—C,A—D—E分别表示甲、小狗与乙的距离y km与甲行进时间x h之间关系的部分函数图象.
(1) 求AB所在直线对应的函数表达式;
(2) 小狗的速度为______ km/h,点E的坐标是______;
(3) 在小狗从出发到它折返后第一次与甲相遇的过程中,当x为何值时,它与乙的距离等于它与甲的距离?
(1) 设AB所在直线的函数表达式为$y_1 = ax + b$,将A(0,4),B(2,0)代入,得$\begin{cases} b = 4, \\ 2k + b = 0, \end{cases}$解得$\begin{cases} k = -2, \\ b = 4, \end{cases}$
∴ AB所在直线的函数表达式为
$y_1 = -2x + 4$
(2)小狗的速度为
12
km/h,点E的坐标是
$(\frac{2}{3},\frac{8}{3})$
;
(3) 在小狗从出发到它折返后第一次与甲相遇的过程中,当x为何值时,它与乙的距离等于它与甲的距离?
∵ 点A,D,E的坐标分别为(0,4),$(\frac{1}{2},0)$,$(\frac{2}{3},\frac{8}{3})$,同理(1),直线DE对应的函数表达式为$y_2 = 16x - 8$,直线AD对应的函数表达式为$y_3 = -8x + 4$,∴ 分两种情况:① $y_1 = 2y_3$,即$-2x + 4 = 2(-8x + 4)$,解得$x = \frac{2}{7}$;② $y_1 = 2y_2$,即$-2x + 4 = 2(16x - 8)$,解得$x = \frac{10}{17}$. 综上所述,当x为$\frac{2}{7}$或$\frac{10}{17}$时,小狗与乙的距离等于其与甲的距离
答案:
(1) 设AB所在直线的函数表达式为$y_1 = ax + b$,将A(0,4),B(2,0)代入,得$\begin{cases} b = 4, \\ 2k + b = 0, \end{cases}$解得$\begin{cases} k = -2, \\ b = 4, \end{cases}$
∴ AB所在直线的函数表达式为$y_1 = -2x + 4$
(2)12,$(\frac{2}{3},\frac{8}{3})$
(3)
∵ 点A,D,E的坐标分别为(0,4),$(\frac{1}{2},0)$,$(\frac{2}{3},\frac{8}{3})$,同理
(1),直线DE对应的函数表达式为$y_2 = 16x - 8$,直线AD对应的函数表达式为$y_3 = -8x + 4$,
∴ 分两种情况:① $y_1 = 2y_3$,即$-2x + 4 = 2(-8x + 4)$,解得$x = \frac{2}{7}$;② $y_1 = 2y_2$,即$-2x + 4 = 2(16x - 8)$,解得$x = \frac{10}{17}$. 综上所述,当x为$\frac{2}{7}$或$\frac{10}{17}$时,小狗与乙的距离等于其与甲的距离