10. 一次函数$y= kx-b$(k,b为常数且$k≠0$,$b≠0$)的图象与$y= 3x$的图象相交于点N(m,-6),则关于x的方程$kx-b= 3x的解为x= $
-2
.
答案:-2
解析:
因为点$N(m,-6)$在$y = 3x$的图象上,所以将$y=-6$代入$y = 3x$,得$-6=3m$,解得$m=-2$。
一次函数$y=kx - b$与$y = 3x$的图象相交于点$N(-2,-6)$,所以关于$x$的方程$kx - b=3x$的解为$x=-2$。
$-2$
11. 已知一次函数的图象经过点(1,2),(4,-4),(m,3),求m的值.
答案:设这个一次函数表达式为$y = kx + b(k \neq 0)$.
∵ 一次函数图象过点(1,2)和(4,-4)
∴ $\begin{cases} k + b = 2, \\ 4k + b = -4, \end{cases}$解得$\begin{cases} k = -2, \\ b = 4, \end{cases}$
∴ $y = -2x + 4$.
∴ $-2m + 4 = 3$,解得$m = \frac{1}{2}$
12. 已知函数$y= kx+b$的图象经过第一、二、三象限,且点(3,1)在该直线上,求k的取值范围.
答案:把(3,1)代入$y = kx + b$得$3k + b = 1$,$b = -3k + 1$,函数$y = kx + b$的图象经过第一、二、三象限,所以$k > 0$,$b > 0$,即$-3k + 1 > 0$,所以k的取值范围为$0 < k < \frac{1}{3}$
解析:
解:把点$(3,1)$代入$y = kx + b$,得$3k + b = 1$,则$b = -3k + 1$。
因为函数$y = kx + b$的图象经过第一、二、三象限,所以$k > 0$且$b > 0$。
即$-3k + 1 > 0$,解得$k < \frac{1}{3}$。
综上,$k$的取值范围为$0 < k < \frac{1}{3}$。
13. 如图,已知一次函数$y= x-2$的图象与y轴交于点A,一次函数$y= 4x+b$的图象与y轴交于点B,且与x轴以及一次函数$y= x-2$的图象分别交于点C,D,点D的坐标为(-2,m).
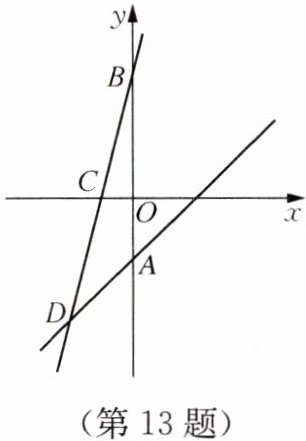
(1) 关于x,y的方程组$\begin{cases}y-x= -2\\y-4x= b\end{cases} $的解为
$\begin{cases} x = -2 \\ y = -4 \end{cases}$
.
(2) 关于x的不等式$x-2≥4x+b$的解集为
$x \leqslant -2$
.
(3) 在x轴上是否存在点E,使得以C,D,E为顶点的三角形是直角三角形?若存在,直接写出点E的坐标;若不存在,请说明理由.
点E的坐标为(-2,0)或(-18,0)
答案:
(1) $\begin{cases} x = -2 \\ y = -4 \end{cases}$
(2) $x \leqslant -2$
(3) 点E的坐标为(-2,0)或(-18,0)