1. 如图,在长方形ABCD中,AB= 2,BC= 3,动点P沿折线BCD从点B开始运动到点D.设点P运动的路程为x,△ADP的面积为y,那么y与x之间函数关系的图象大致是(
D
)
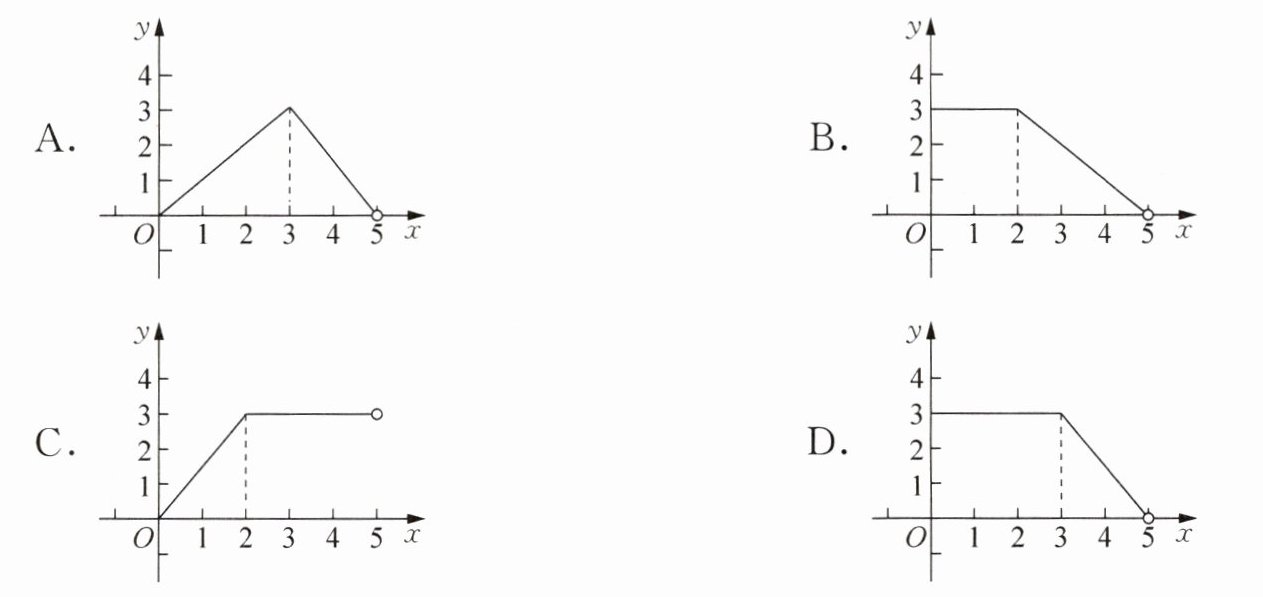

A.
B.
C.
D.
答案:D
解析:
当点P在BC上运动时(0≤x≤3),DP=AB=2,AD=BC=3,△ADP的面积y= $\frac{1}{2} × AD × AB = \frac{1}{2} × 3 × 2 = 3$,此时y为常数3;
当点P在CD上运动时(3<x≤5),CP=x-3,DP=CD-CP=2-(x-3)=5-x,△ADP的面积y= $\frac{1}{2} × AD × DP = \frac{1}{2} × 3 × (5 - x) = -\frac{3}{2}x + \frac{15}{2}$,此时y随x增大而减小。
函数图象先为水平线段(y=3,0≤x≤3),再为下降线段(3<x≤5),符合选项D。
D
2. 若直线BC和函数$y= x+3$的图象平行,其中点B的坐标为(-2,3),则直线BC对应的函数表达式为(
C
)
A.$y= -x+5$
B.$y= -x+4$
C.$y= x+5$
D.$y= x+4$
答案:C
解析:
∵直线BC与函数$y = x + 3$的图象平行,
∴设直线BC的函数表达式为$y = x + b$。
∵点B$(-2, 3)$在直线BC上,
∴将$x=-2$,$y=3$代入$y = x + b$,得$3=-2 + b$,
解得$b=5$,
∴直线BC对应的函数表达式为$y = x + 5$。
C
3. 如果一个正比例函数的图象经过不同象限的两点A(3,m),B(n,-2),那么一定有(
B
).
A.$m>0$,$n>0$
B.$m>0$,$n<0$
C.$m<0$,$n>0$
D.$m<0$,$n<0$
答案:B
解析:
设正比例函数解析式为$y=kx(k\neq0)$。
因为函数图象经过点$A(3,m)$,所以$m=3k$;经过点$B(n,-2)$,所以$-2=kn$,即$n=-\dfrac{2}{k}$。
由于$A$、$B$是不同象限的两点,分情况讨论:
若$k>0$,则正比例函数图象经过第一、三象限。此时$m=3k>0$,$n=-\dfrac{2}{k}<0$,点$A(3,m)$在第一象限,点$B(n,-2)$在第三象限,符合不同象限。
若$k<0$,则正比例函数图象经过第二、四象限。此时$m=3k<0$,$n=-\dfrac{2}{k}>0$,点$A(3,m)$在第四象限,点$B(n,-2)$在第二象限,符合不同象限。
综上,无论$k$正负,总有$m$和$n$异号。结合选项,只有$B$选项$m>0$,$n<0$符合条件。
B
4. 已知$A(x_{1},y_{1})$,$B(x_{2},y_{2})是函数y= (m+1)x-1$图象上相异的两点,如果$(y_{1}-y_{2})(x_{1}-x_{2})<0$,那么m的取值范围是(
B
)
A.$m>-1$
B.$m<-1$
C.$m≥-1$
D.$m≤-1$
答案:B
解析:
因为$A(x_{1},y_{1})$,$B(x_{2},y_{2})$是函数$y=(m + 1)x-1$图象上相异的两点,所以$y_{1}=(m + 1)x_{1}-1$,$y_{2}=(m + 1)x_{2}-1$。
$y_{1}-y_{2}=(m + 1)x_{1}-1-[(m + 1)x_{2}-1]=(m + 1)(x_{1}-x_{2})$。
已知$(y_{1}-y_{2})(x_{1}-x_{2})<0$,则$(m + 1)(x_{1}-x_{2})^{2}<0$。
因为$A$,$B$是相异两点,所以$x_{1}≠x_{2}$,即$(x_{1}-x_{2})^{2}>0$。
所以$m + 1<0$,解得$m<-1$。
B
5. 关于函数$y= (k-3)x+k$(k为常数)有下列结论:①当$k≠3$时,此函数是一次函数;②无论k取什么值,函数图象必经过点(-1,3);③若图象经过第二、三、四象限,则k的取值范围是$k<0$;④若函数图象与x轴的交点始终在正半轴,则k的取值范围是$0<k<3$.其中,正确结论的个数是(
D
)
A.1
B.2
C.3
D.4
答案:D
解析:
①当$k≠3$时,$x$的系数$k - 3≠0$,此函数是一次函数,正确;
②将$x=-1$代入$y=(k - 3)x + k$,得$y=-(k - 3)+k=3$,无论$k$取何值,函数图象必过点$(-1,3)$,正确;
③若图象过第二、三、四象限,则$\begin{cases}k - 3<0\\k<0\end{cases}$,解得$k<0$,正确;
④令$y=0$,则$x=-\frac{k}{k - 3}$,交点在正半轴,$-\frac{k}{k - 3}>0$,即$\frac{k}{k - 3}<0$,解得$0<k<3$,正确。
正确结论的个数是4。
D
6. 对于一次函数$y= -2x+4$,当$-2≤x≤4$时,函数y的取值范围是
-4≤y≤8
.
答案:-4≤y≤8
解析:
解:对于一次函数$y = -2x + 4$,$k=-2<0$,函数值$y$随$x$的增大而减小。
当$x=-2$时,$y=-2×(-2)+4=8$;
当$x=4$时,$y=-2×4 + 4=-4$。
所以当$-2\leq x\leq4$时,$-4\leq y\leq8$。
$-4\leq y\leq8$
7. 若一次函数$y= (m-1)x+3m-2$的图象不经过第三象限,则实数m的取值范围为
$\frac{2}{3} \leqslant m < 1$
.
答案:$\frac{2}{3} \leqslant m < 1$
8. 若关于x的方程$kx+b= 0(k≠0)$的解是$x= 1$,则函数$y= kx+b$的图象一定经过点
(1,0)
.
答案:(1,0)
9. 如图,在平面直角坐标系中,函数$y= -\frac{4}{3}x+4$的图象与x轴、y轴分别交于点A,B,点M在y轴上(不与点B重合),若将△ABM沿直线AM翻折,点B恰好落在x轴正半轴上,则点M的坐标为
(0,-6)
.
答案:(0,-6)
解析:
在函数$y = -\frac{4}{3}x + 4$中,令$x = 0$,得$y = 4$,则$B(0,4)$;令$y = 0$,得$0=-\frac{4}{3}x + 4$,解得$x = 3$,则$A(3,0)$,$OA=3$,$OB=4$,由勾股定理得$AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{3^{2}+4^{2}} = 5$。
设点$B$翻折后落在$x$轴正半轴上的点为$B'(t,0)$,$t>0$,由翻折性质知$AB'=AB = 5$,$MB'=MB$。
因为$A(3,0)$,所以$AB'=|t - 3| = 5$,又$t>0$,解得$t=8$($t=-2$舍去),即$B'(8,0)$。
设$M(0,m)$,$m\neq4$,则$MB=|m - 4|$,$MB'=\sqrt{(8 - 0)^{2}+(0 - m)^{2}}=\sqrt{64 + m^{2}}$。
由$MB'=MB$得$\sqrt{64 + m^{2}}=|m - 4|$,两边平方:$64 + m^{2}=(m - 4)^{2}$,展开得$64 + m^{2}=m^{2}-8m + 16$,化简得$8m=-48$,解得$m=-6$。
故点$M$的坐标为$(0,-6)$。