6. 已知函数$y= mx(m \neq 0)的图象与函数y= kx+4(k \neq 0)的图象的交点坐标为P(1,3)$,则方程组$\begin{cases} y= mx \\ y= kx-4 \end{cases} $的解为
$\begin{cases} x=-1 \\ y=-3 \end{cases}$
.
答案:{x=-1, y=-3}
解析:
因为函数$y = mx(m \neq 0)$的图象过点$P(1,3)$,所以$3 = m×1$,解得$m = 3$,即$y = 3x$。
函数$y = kx + 4(k \neq 0)$的图象过点$P(1,3)$,所以$3 = k×1 + 4$,解得$k = -1$。
则方程组$\begin{cases}y = mx \\ y = kx - 4\end{cases}$为$\begin{cases}y = 3x \\ y = -x - 4\end{cases}$。
联立方程得$3x=-x - 4$,$4x=-4$,$x=-1$。
将$x=-1$代入$y = 3x$,得$y=-3$。
所以方程组的解为$\begin{cases}x=-1 \\ y=-3\end{cases}$
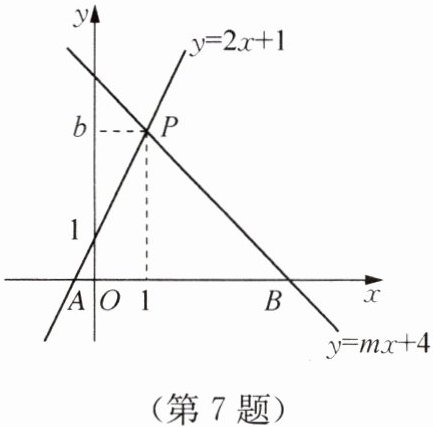
7. 如图,函数$y= 2x+1的图象与函数y= mx+4的图象交于点P(1,b)$,与$x轴分别交于A$,$B$两点.
(1) 求$b$,$m$的值,并结合图象写出关于$x$,$y的方程组\begin{cases} 2x-y= -1 \\ mx-y= -4 \end{cases} $的解;
(2) 求$\triangle ABP$的面积;
(3) 若垂直于$x轴的直线l与一次函数y= 2x+1$的图象、$y= mx+4的图象分别交于点C$,$D$,且线段$CD$的长为2,直接写出直线$l$对应的函数表达式.
]
答案:
(1) 把点P(1,b)代入y=2x+1,得b=2+1=3,把点P(1,3)代入y=mx+4,得m+4=3,
∴ m=-1.
∵ 直线l₁:y=2x+1与直线l₂:y=mx+4相交于点P(1,3),
∴ 方程组{2x-y=-1, mx-y=-4}的解为{x=1, y=3}
(2) S△ABP=1/2AB·h=1/2×9/2×3=27/4
(3) 设l对应的函数表达式为x=a,则交点C为(a,2a+1),交点D为(a,-a+4).
∵ CD=2,
∴ |2a+1-(-a+4)|=2,即|3a-3|=2,
∴ 3a-3=2或3a-3=-2,
∴ a=5/3或a=1/3,即函数表达式为x=1/3或x=5/3