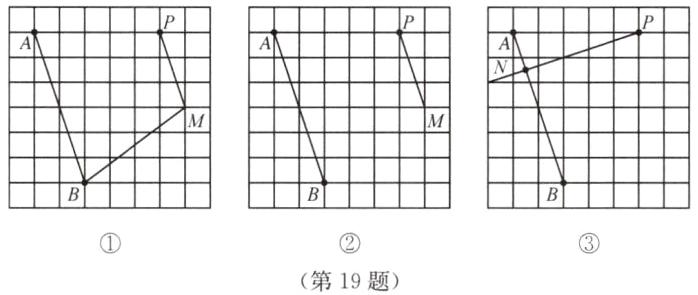
16. 对于平面内的$\angle M和\angle N$,若存在一个常数$k(k>0)$,使得$\angle M+k\angle N= 360^\circ$,则称$\angle N为\angle M的k$系补周角. 如若$\angle M= 90^\circ$,$\angle N= 45^\circ$,则$\angle N为\angle M$的6系补周角. 如图,在平面内$AB// CD$,$E是AB$,$CD$之间的一点,连接$BE$,$DE$,若$\angle D= 60^\circ$,$\angle B是\angle E$的5系补周角,则$\angle E= $
110
.
答案:110
解析:
过点E作EF//AB,
因为AB//CD,所以EF//CD,
所以∠ABE+∠BEF=180°,∠CDE+∠DEF=180°,
所以∠ABE+∠BEF+∠CDE+∠DEF=360°,
即∠B+∠E+∠D=360°,
因为∠D=60°,所以∠B+∠E=300°,
因为∠B是∠E的5系补周角,所以∠E+5∠B=360°,
联立得:$\begin{cases}∠B + ∠E = 300° \\ ∠E + 5∠B = 360°\end{cases}$,
解得∠E=290°(舍去),
过点E作EF//AB交BC于F,
因为AB//CD,所以EF//CD,
所以∠BEF=∠B,∠DEF=∠D,
所以∠E=∠BEF+∠DEF=∠B+∠D,
即∠B=∠E-∠D,
因为∠D=60°,所以∠B=∠E-60°,
因为∠B是∠E的5系补周角,所以∠E+5∠B=360°,
所以∠E+5(∠E-60°)=360°,
6∠E=660°,
∠E=110°。
110
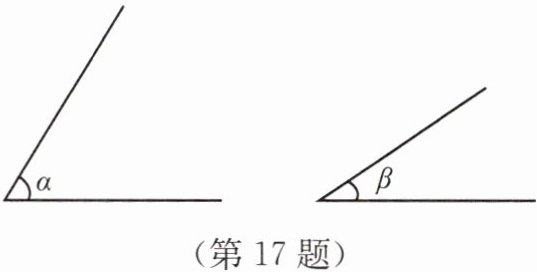
17. 如图,已知$\angle \alpha$,$\angle \beta$,利用直尺和圆规作$\angle AOB$,使$\angle AOB的大小为\angle \alpha +\angle \beta$.(不写作法,保留作图痕迹)
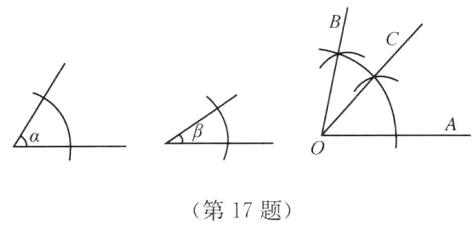
答案:如图,∠AOB即为所求
18. (1)如图①,点$C$,$D在线段AB$上,$D是线段AB$的中点,$AC= \frac{1}{3}AD$,$CD= 4$,求线段$AB$的长;
(2)如图②,$O是直线AB$上的一点,$OD是\angle AOC$的平分线,$OE是\angle COB$的平分线,若$\angle AOD= 14^\circ$,求$\angle DOE$,$\angle BOE$的大小.

答案:
(1)因为AC = $\frac{1}{3}$AD,所以CD = $\frac{2}{3}$AD,因为CD = 4,所以$\frac{2}{3}$AD = 4,解得AD = 6,因为D是线段AB的中点,所以AB = 2AD = 12。
(2)因为OD是∠AOC的平分线,所以∠AOD = ∠COD = 14°,∠AOC = 2∠AOD = 28°,所以∠BOC = 180° - ∠AOC = 152°,因为OE是∠COB的平分线,所以∠BOE = ∠COE = $\frac{1}{2}$∠BOC = 76°,所以∠DOE = ∠COD + ∠COE = 14° + 76° = 90°。
19. 如图,每个小方格都是边长为1的正方形,$A$,$B$,$P$都是格点.
(1)画线段$PM// AB$,且$PM= \frac{1}{2}AB$;
(2)连接$AP和BM$,则四边形$ABMP$的面积是______;
(3)在$AB上找一点N$,使线段$PN$的长度最短.

答案:(1)如图,点M即为所求。
(2)如图,S四边形ABPM = 6×6 - $\frac{1}{2}$×6×2 - $\frac{1}{2}$×4×3 - $\frac{1}{2}$×1×3 = $\frac{45}{2}$。
(3)如图,点N即为所求