20. 如图,已知$\angle E= \angle F$,$\angle A= \angle D$. 判断$\angle 1$,$\angle 2$是否相等.
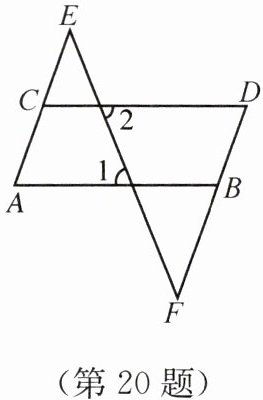
答案:因为∠E = ∠F,所以AE//DF,所以∠A = ∠ABF,因为∠A = ∠D,所以∠D = ∠ABF,所以AB//CD,所以∠1 = ∠2。
21. 如图,$AD\perp BC$,$EG\perp BC$,垂足分别为$D$,$G$,$\angle E= \angle 3$,判断$AD是否平分\angle BAC$,并说明理由.

答案:因为AD⊥BC,EG⊥BC,所以∠ADC = ∠EGC = 90°(垂直定义),所以AD//EG(同位角相等,两直线平行),所以∠1 = ∠E(两直线平行,同位角相等),∠2 = ∠3(两直线平行,内错角相等),因为∠3 = ∠E(已知),所以∠1 = ∠2(等量代换),所以AD平分∠BAC(角平分线定义)。
22. 已知$BC// OA$,$\angle B= \angle A= 100^\circ$,试回答下列问题:
(1)如图①,判断$OB$,$AC$是否平行.
(2)如图②,若点$E$,$F在BC$上,且满足$\angle FOC= \angle AOC$,并且$OE平分\angle BOF$. 求$\angle EOC$的度数.
(3)在(2)的条件下,若平行移动$AC$,如图③,那么$\angle OFB与\angle OCB$的度数之比是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

答案:
(1)因为BC//OA,所以∠B + ∠O = 180°,又因为∠B = ∠A,所以∠A + ∠O = 180°,所以OB//AC。
(2)因为∠B + ∠BOA = 180°,∠B = 100°,所以∠BOA = 80°,因为OE平分∠BOF,所以∠BOE = ∠EOF,又因为∠FOC = ∠AOC,所以∠EOC = ∠EOF + ∠FOC = $\frac{1}{2}$(∠BOF + ∠FOA) = $\frac{1}{2}$∠BOA = 40°。
(3)结论:∠OFB与∠OCB的度数之比不发生变化。理由:因为BC//OA,所以∠FCO = ∠COA,又因为∠FOC = ∠AOC,所以∠FOC = ∠FCO,所以∠OFB = ∠FOC + ∠FCO = 2∠OCB,所以∠OFB与∠OCB的度数之比是2:1。