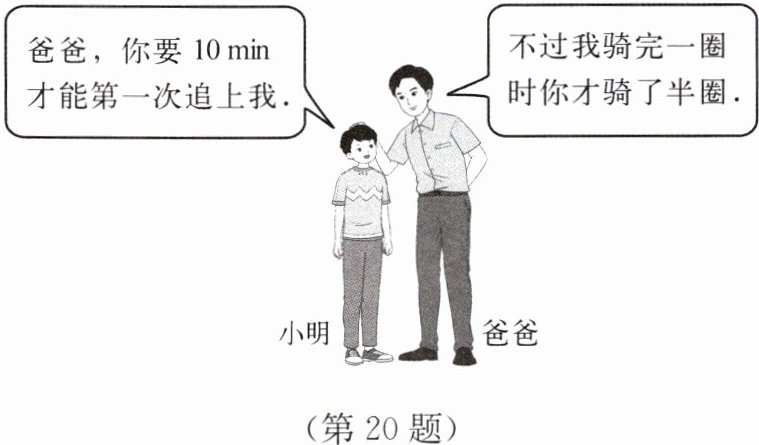
20. 周末,小明和爸爸在3000m的环形绿道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如图所示的对话.
(1)请根据他们的对话内容,求出小明的骑行速度;
(2)爸爸第一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸在跑道上相距1000m?
答案:(1)设小明的骑行速度为x m/min,则爸爸的骑行速度为2x m/min,根据题意,得$10(2x-x)=1500$,解得$x=150$。答:小明的骑行速度为150 m/min;(2)设在第二次相遇前,再经过y min,小明和爸爸在绿道上相距1000 m,① 爸爸又比小明多骑了1000 m,根据题意,得$2×150y-150y=1000$,解得$y=\frac{20}{3}$;② 爸爸又比小明多骑了$(3000-1000)$m,根据题意,得$2×150y-150y=3000-1000$,解得$y=\frac{40}{3}$。答:在第二次相遇前,再经过$\frac{20}{3}$min或$\frac{40}{3}$min,小明和爸爸在跑道上相距1000 m
解析:
(1)设小明的骑行速度为$x\ m/min$,由爸爸骑完一圈时小明骑了半圈,可得爸爸的骑行速度为$2x\ m/min$。根据题意,得$10(2x - x)=3000$,解得$x = 300$。答:小明的骑行速度为$300\ m/min$;
(2)设在第二次相遇前,再经过$y\ min$,小明和爸爸在绿道上相距$1000\ m$。爸爸速度为$2×300 = 600\ m/min$。①爸爸比小明多骑$1000\ m$,$600y-300y=1000$,解得$y=\frac{10}{3}$;②爸爸比小明多骑$3000 - 1000=2000\ m$,$600y - 300y=2000$,解得$y=\frac{20}{3}$。答:再经过$\frac{10}{3}\ min$或$\frac{20}{3}\ min$,小明和爸爸相距$1000\ m$。
21. 阅读材料并解决问题:
若关于$x的一元一次方程ax = b的解满足x = b + a$,则我们称该方程为“友好方程”.
例如:方程$2x = -4的解为x = -2$,因为$a = 2$,$b = -4$,所以有$-2= -4 + 2$,即$x = b + a$,则方程$2x = -4$为“友好方程”.
运用上述定义解决问题:
(1)①$3x = -4.5$,②$\frac{1}{3}x= -1$,③$-2x = 4$三个方程中,为“友好方程”的是______
①
(填序号);
(2)若关于$x的一元一次方程4x = b$是“友好方程”,求$b$的值;
$b=-\frac{16}{3}$
(3)若关于$x的一元一次方程-3x = mn + n$($n≠0$)是“友好方程”,且它的解为$x = n$,求$m与n$的值.
$m=-4$,$n=-\frac{3}{4}$
答案:(1)①;(2)$b=-\frac{16}{3}$;(3)$m=-4$,$n=-\frac{3}{4}$
解析:
(1)①
(2)解:方程$4x = b$的解为$x = \frac{b}{4}$。
因为该方程是“友好方程”,所以$\frac{b}{4}=b + 4$。
解得$b=-\frac{16}{3}$。
(3)解:因为方程$-3x = mn + n$的解为$x = n$,所以$-3n=mn + n$。
又因为该方程是“友好方程”,所以$n=mn + n+(-3)$,即$n=mn + n - 3$,化简得$mn=3$。
将$mn=3$代入$-3n=mn + n$,得$-3n=3 + n$,解得$n=-\frac{3}{4}$。
将$n=-\frac{3}{4}$代入$mn=3$,得$m×(-\frac{3}{4})=3$,解得$m=-4$。
所以$m=-4$,$n=-\frac{3}{4}$。